Patient Knowledge Distillation for BERT Model Compression 리뷰

EMNLP 2019에 Accept된 마이크로소프트에서 나온 PKD (Patient Knowledge Distillation) 방식의 Model Compression 논문이다. arxiv 링크는 https://arxiv.org/abs/1908.09355이고 코드는 GitHub - intersun/PKD-for-BERT-Model-Compression에 있다.

PKD는 두 전략을 취하는데, 1. PKD-Last: learning from last K layers, 2: PKD-Skip: learning from every K layers이다. 위의 전략을 취해서 model accuracy 하락 없이 Training을 굉장히 효율적으로 할 수 있었다고 한다.

1. Introduction

  • teacher를 lightweight studnet model로 PKD 방식을 이용해서 만들어본다.
  • 기존 KD와 다르게 Patient를 적용헀다.
    • teacher의 last layer만 학습하는 것이 아니라 다른 전 레이어도 학습하도록 했다.

Language Model Pre-training

  • 패스

Model Compression & Knowledge Distillation

3. Patient Knowledge Distillation

3.1. Distillation Objective

  • Teacher: BERT, Student: BERT_k로 표기, Bert base는 BERT_12, Bert large는 BERT_24

  • Teacher 학습

    \[\hat \theta ^t = \text{arg}\min_\theta \sum_{i \in [N]} L^t_{CE} (x_i, y_i; [\theta_{BERT_{12}}, W])\]
    • t : teacher
    • [N] : Set {1,2,3, … N}

  • Output Probability from teacher

    \[\hat {y_i} = P^t (y_i\vert x_i) = softmax(\frac {W \cdot BERT_{12} (x_i; \hat \theta ^t)} T)\]
    • T: Temperature used in KD

  • Student, Teacher의 output probability의 distance 계산

    \[L_{DS} = - \sum_{i \in [N]} \sum_{c \in C} [P^t (y_i = c \vert x_i;\hat \theta ^t) \cdot \log P^s (y_i = c |x_i ; \theta ^s)]\]
  • 물론 Teacher의 Soft Target을 학습하는 것도 좋지만, hard target도 맞춰야 하니 Task Specific에 대해서도 Cross Entropy를 추가한다.
  • 따라서 최종 objective는 \(L_{KD} = (1 - \alpha) L^s_{CE} + \alpha L_{DS}\)가 된다.

3.2. Patient Teacher for Model Compression

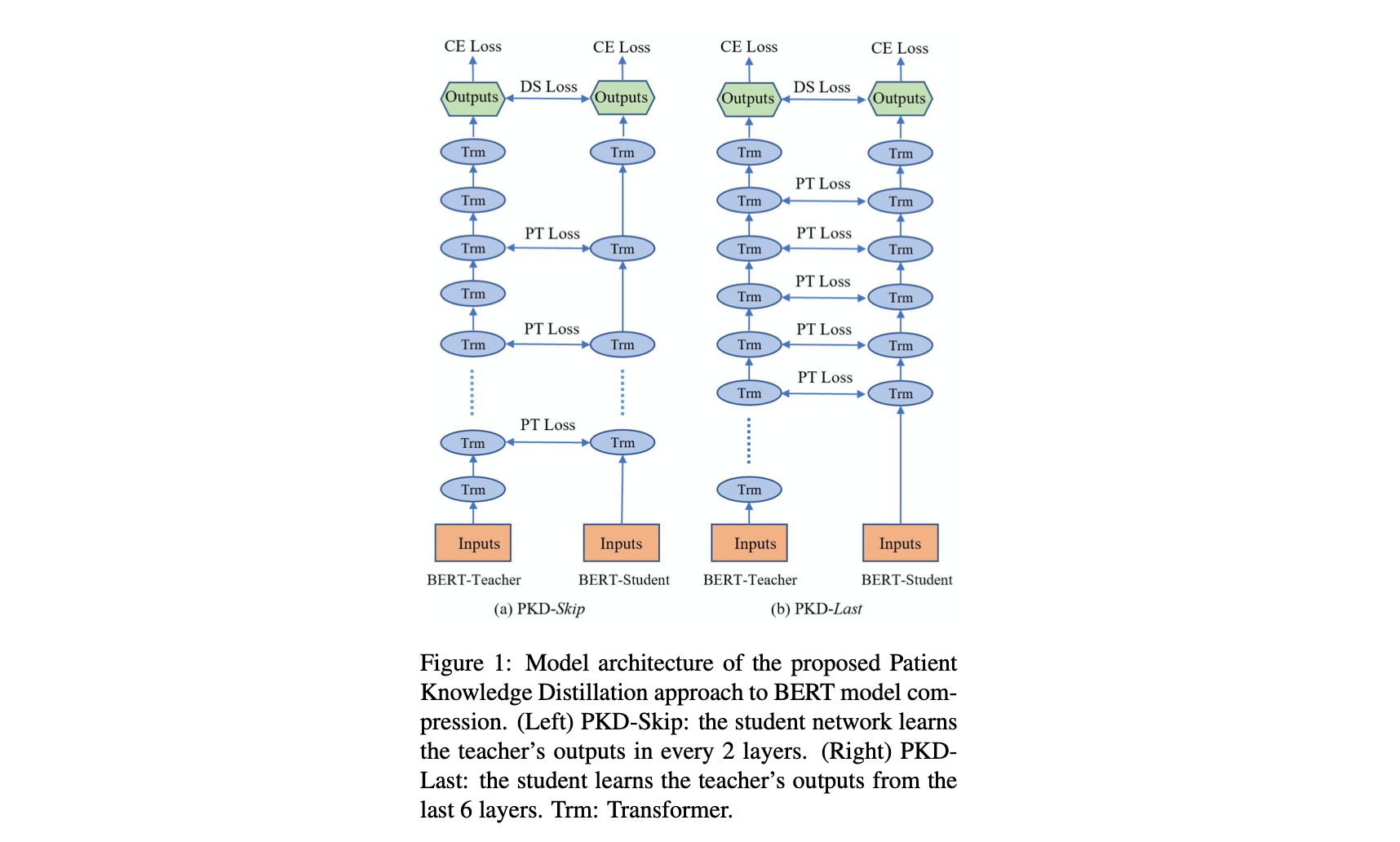
  • KD 중 student가 overfitting할 수도 있기 때문에 patient mechanism을 넣어준다.

  • Teacher Model의 중간 레이어들의 [CLS] 토큰 representation들을 가져온다.

    \[h_i = [h_{i_1}, h_{i_2}, ..., h_{i_k}] = BERT_k(x_i) \in \mathbb R^{k \times d}\]
  • 그렇게 해서 Stduent의 결과와 Mean-square loss를 계산한다. \(L_{PT}\)
  • final loss: \(L_{PKD} = (1 - \alpha) L^s_{CE} + \alpha L_{DS} + \beta L_{PT}\)

4. Experiments

4.1. Datasets

  • GLUE

4.2. Baselines and Training Details

  • Teacher 모델로 BERT_12를 각각 태스크에 대해 독립적으로 다 fine-tuning시킴
  • Student 모델로 BERT_3, BERT_6을 준비.
    • 첫 k 레이어로 initialize
  • Temperature 는 {5, 10, 20}사이에서 고름, \(\alpha\)도 {0.2, 0.5, 0.7} 사이에서 고름, \(\beta\)는 {10, 100, 500, 1000} 사이에서 고름

4.3. Experimental Results

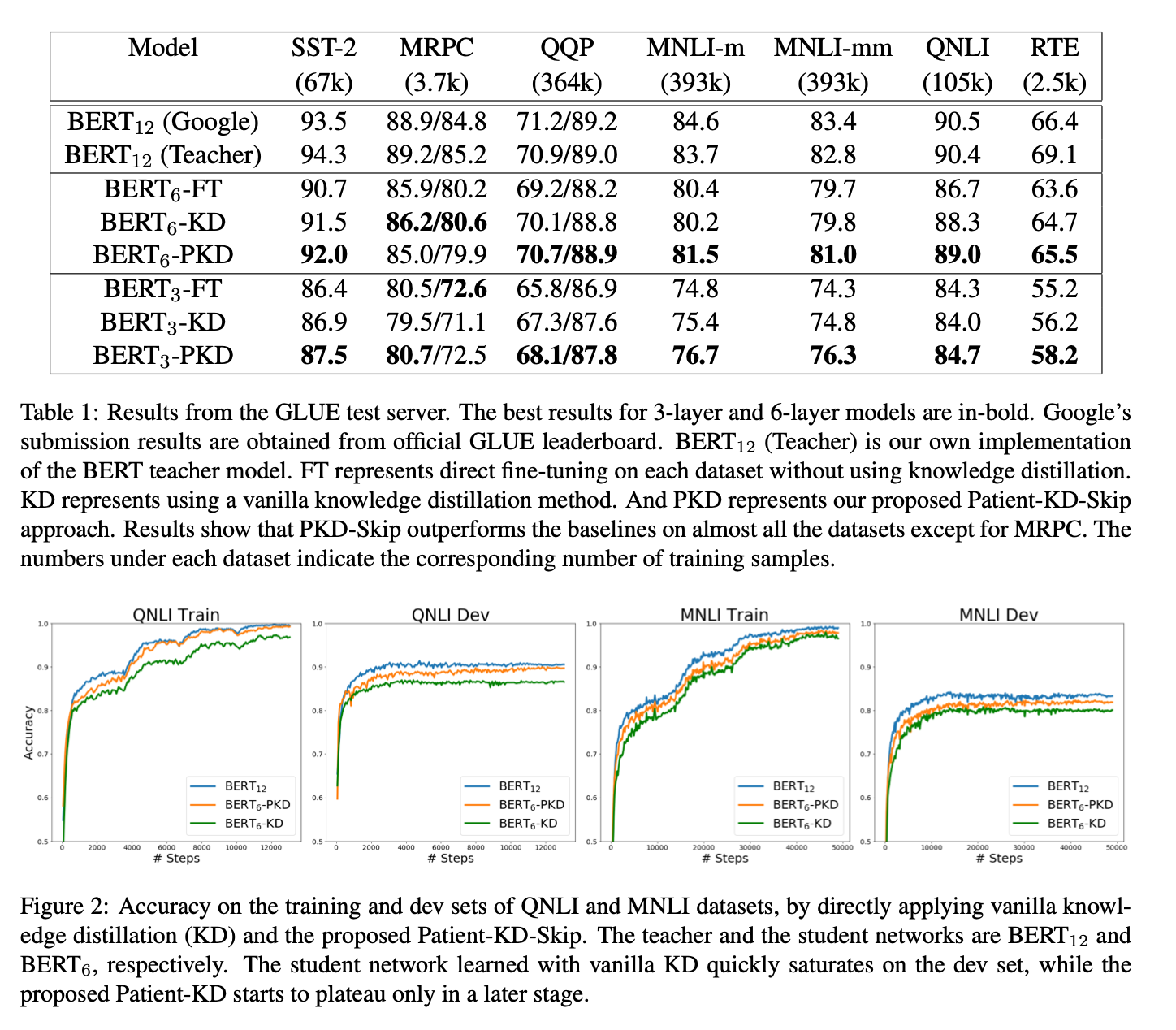
  • 그냥 BERT_small을 Fine tuning한 것보다 훨씬 잘나오는 결과를 볼 수 있다. 하지만, 그래도 MRPC 같은 태스크들은 좀 성능이 떨어진다.
  • 그래도 좋은 점은 QQP, MNLI-m, MNLI-mm, QNLI 같은 태스크는 얼마 떨어지지 않았는데, 이 태스크들의 공통점이 60k 이상의 sample이 있다는 것들이고, training data가 많을 때 잘된다는 것을 어느정도 증명한 셈이다.
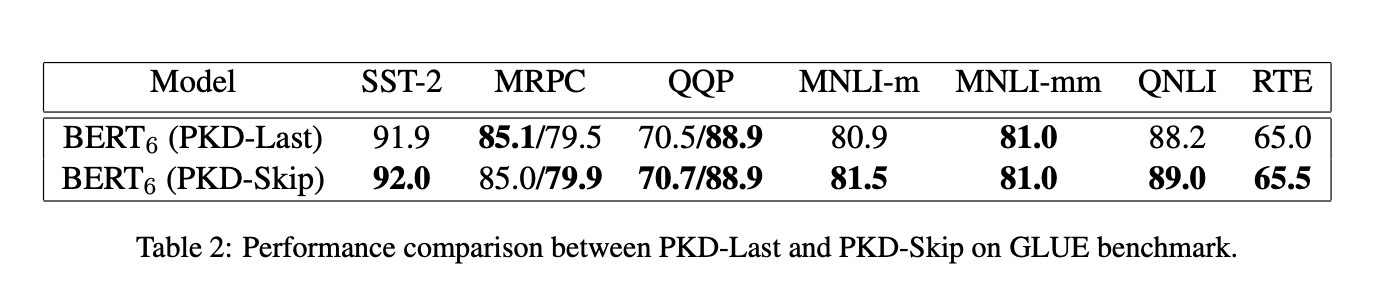
  • PKD-Last와 PKD-Skip을 비교해보았을 때는 PKD-Skip이 좀 더 나은 결과를 보인다.
    • 아마 PKD-Skip이 조금 더 low-level ~ high-level까지 diverse한 representation과 richer semantics을 잡아낼 수 있어서 그런 것 같다고 한다.

4.4. Analysis of Model Efficiency

  • Titan RTX GPU에서 batch 128, seq length 128, FP16으로 테스트했을 때 아래와 같은 결과를 보였다고 ㅎ나다.

4.5. Does a Better Teacher Help?

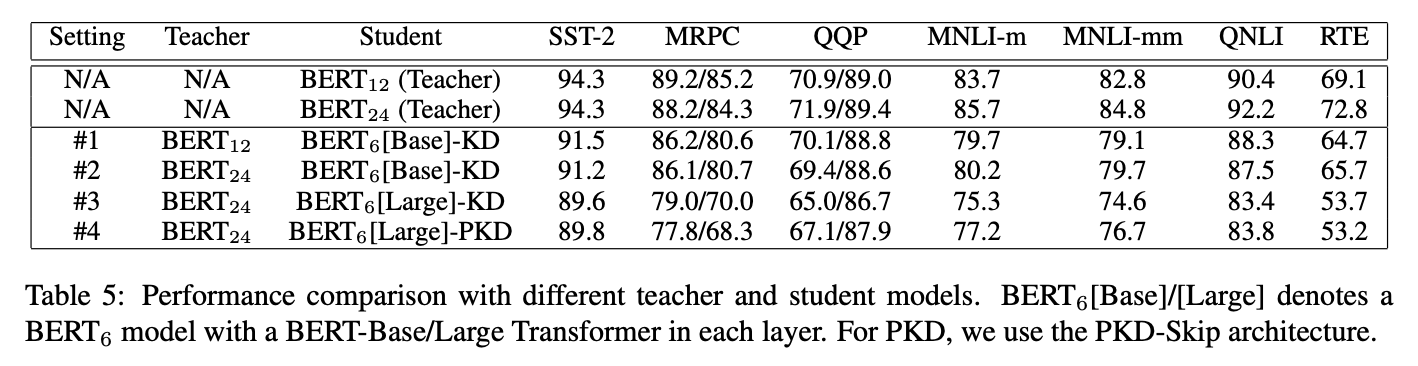
  • 꼭 그렇지만은 않다.
  • BERT12가 더 잘 가르칠 때도 많다.
  • 오히려 #3은 #1보다 나쁜 성능을 보인다.
  • 하지만, #3, #4를 비교해볼 때 PKD는 Teacher Model에 상관없이 잘되는 것으로 보인다.

5. Conclusion

  • Future works
    • Designing more sophisticated distance metrics for loss function
    • investigate Patient-KD in more complex settings such as multi-task learning and meta learning.
April 16, 2020
Tags: paper