This post is a note for the paper “MIXOUT: Effective Regularization to Finetune Large-scale Pretrained Language Model” (Lee et al., 2019).

TL;DR

• “Mixout” is a technique that stochastically mixes the parameters of two models (in this paper, two models are usually the pretrained model and the model that is in finetuning).
• Applying mixout significantly stabilizes the results of finetuning BERT_large on small training sets.
• Pytorch implementation from the author: https://github.com/bloodwass/mixout
• Forward function is here (bloodwass/mixout/mixout.py#L59)

Abstract

• In this paper, the authors introduce a new regularization technique, “mixout”, motivated by “dropout”.
• “Mixout” is a technique that stochastically mixes the parameters of two models.
• The authors evaluated this via finetuning BERT_large on downstream tasks in GLUE.

Introduction

• The authors will provide a theoretical understanding of the dropout and its variants, and empirically verify with two experiments.
  1. Train a fully-connected network on EMNIST Digits and finetune it on MNIST.
  2. (Main Experiments) Finetune BERT_large on training sets of GLUE.
• In the ablation study, the authors will perform three experiments.
  1. The effect of the mixout on a sufficient number of training sets.
  2. The effect of a regularization technique for an additional output layer which is not pre-trained.
  3. The effect of the probability of mixout compared to dropout.

Analysis of Dropout and Its Generalization

• Mixconnect
  • If the loss function is strongly convex, mixconnect term can act as an L2 regularizer term.
    • Check this link for a detailed description of Strong Convexity.

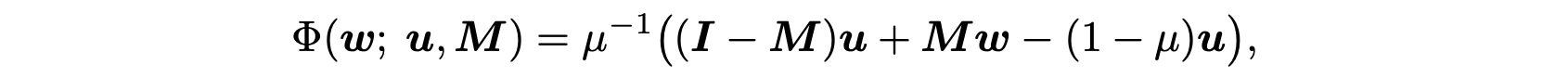
• Mixout
  • The authors propose the mixout as a special case of a mixconnect, which is motivated by the relationship between dropout and dropconnect.
  • Mixout chooses a random mask matrix from Bernoulli(1 - p), so an L2 regularization coefficient is mp/(1 - p). (Check details in the paper)
    • It means that the probability of the mixout can adjust the strength of the L2 penalty.
• Mixout for Pretrained Model
  • When training from scratch, an initial model parameter is usually sampled from a normal/uniform distribution with mean 0 and small variance, but after training, the model parameter is away from the origin with a large t (training step). (Hoffer et al., 2017)
  • Because we obtain pre-trained weight by training on a large corpus, it is often far away from the origin.
  • Dropout L2-penalizes the model parameter for deviating away from the origin rather than the pre-trained weight.
  • So, it should be better to use the mixout to explicitly prevent the deviation from the pre-trained weight.

Verification of Theoretical Results for Mixout on MNIST

• Weight decay is an effective regularization technique to avoid catastrophic forgetting during finetuning(Wiese et al., 2017), and the authors suspect that the mixout has a similar effect with weight decay.
• To verify, the authors pre-trained a fully-connected network and finetuned with replacing dropout with the mixout.
  • Any regularization techniques such as weight decay are not used.
• The result shows that the validation accuracy of the mixout has greater robustness to the choice of probability than that of dropout.

Finetuning a Pretrained Language Model with Mixout

• Notation
  • Weight decay here means an L2 weight decay. (\(wdecay(u, \lambda) = \frac \lambda 2 {\lVert w - u \lVert}^2\), \(w\) is the weight to optimize.)

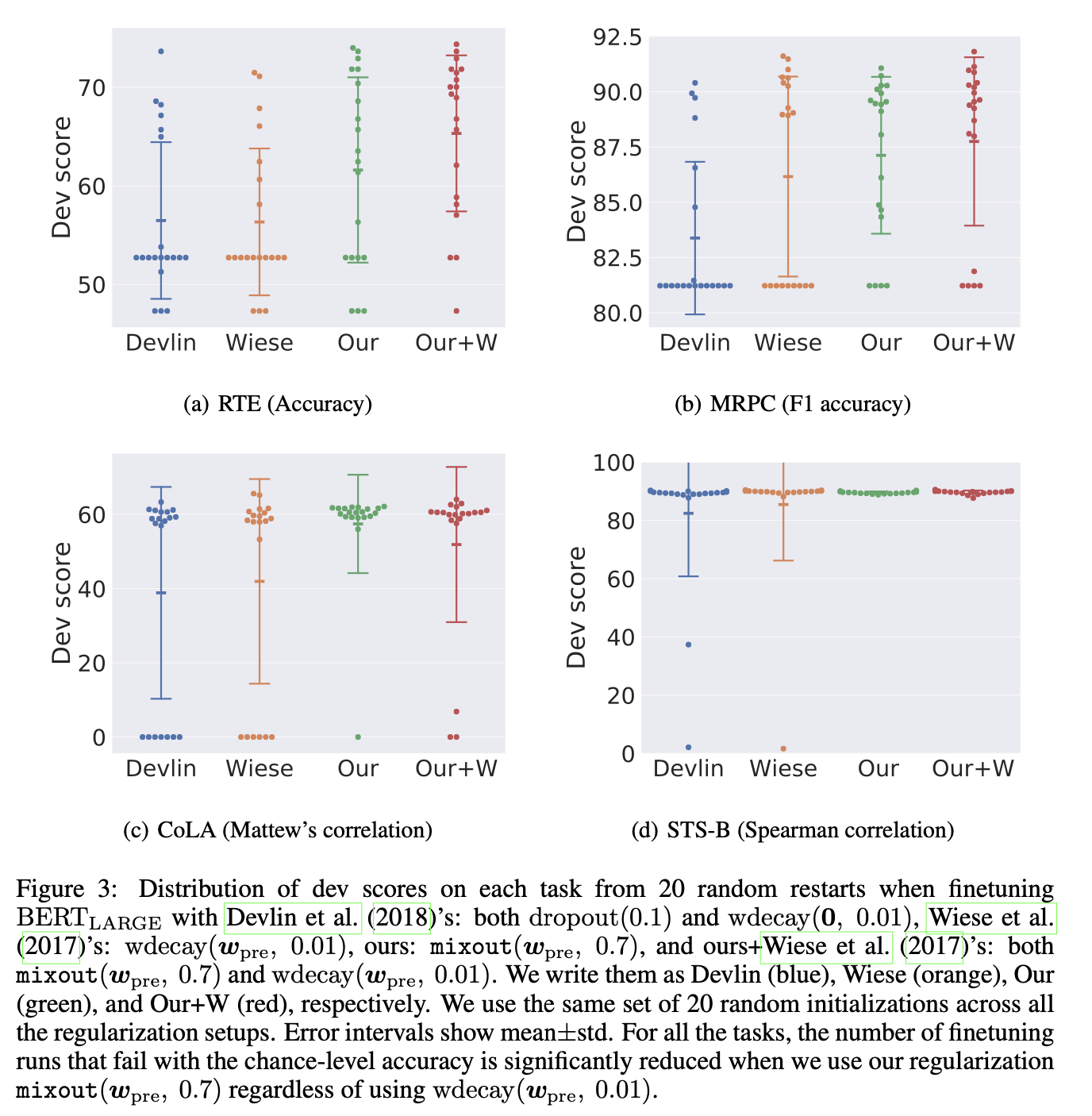
• The authors choose RTE, MRPC, CoLA, and STS-B tasks because these tasks have been observed as unstable to finetune BERT_large (Phang et al., 2018).
• The original regularization strategy (Devlin et al., 2018) for finetuning is using both dropout and \(wdecay(\textbf 0)\).
• But mixout or \(wdecay(w_{pre})\) (\(w_{pre}\) is the pre-trained weight) cannot be used in the output layer because there is no pre-trained weight for the output layer.
• So in this experiment, the regularization strategy for the output layer uses the dropout and \(wdecay(\textbf 0)\).
• Figure 3 shows the results for four regularization strategies.
  1. dropout 0.1 and \(wdecay(\textbf 0, 0.01)\) (Devlin et al., 2018)
  2. \(wdecay(w_{pre}, 0.01)\) (Wiese et al., 2017)
  3. mixout 0.7
  4. 2 + 3
• In short, applying mixout significantly stabilizes the results of finetuning BERT_large on small training sets regardless of whether using \(wdecay(w_{pre}, 0.01)\).

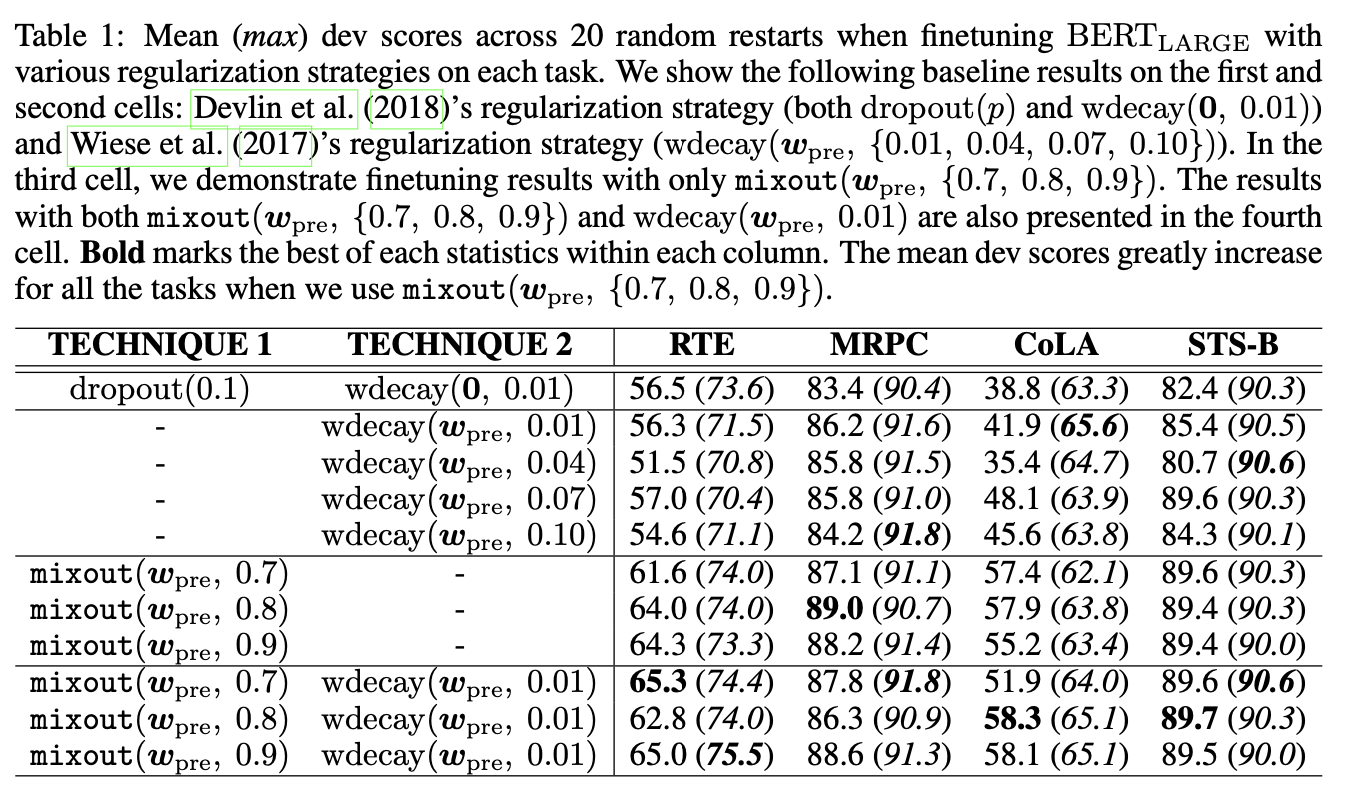
Ablation Study

Mixout with a Sufficient Number of Training Examples

• Tested on SST-2, and the results are similar to each other but slightly better.

Effect of a Regularization Technique for an Additional Output Layer

• In section 3 (Analysis of Dropout and Its Generalization), the authors explained mixout does not differ from dropout when training a randomly initialized layer because weight is sampled from the distribution whose mean and variance are zero and small, respectively.
• Since the expectation value of the initial weight is proportional to the dimensionality of the layer, mixout behaves differently from dropout when training from scratch.

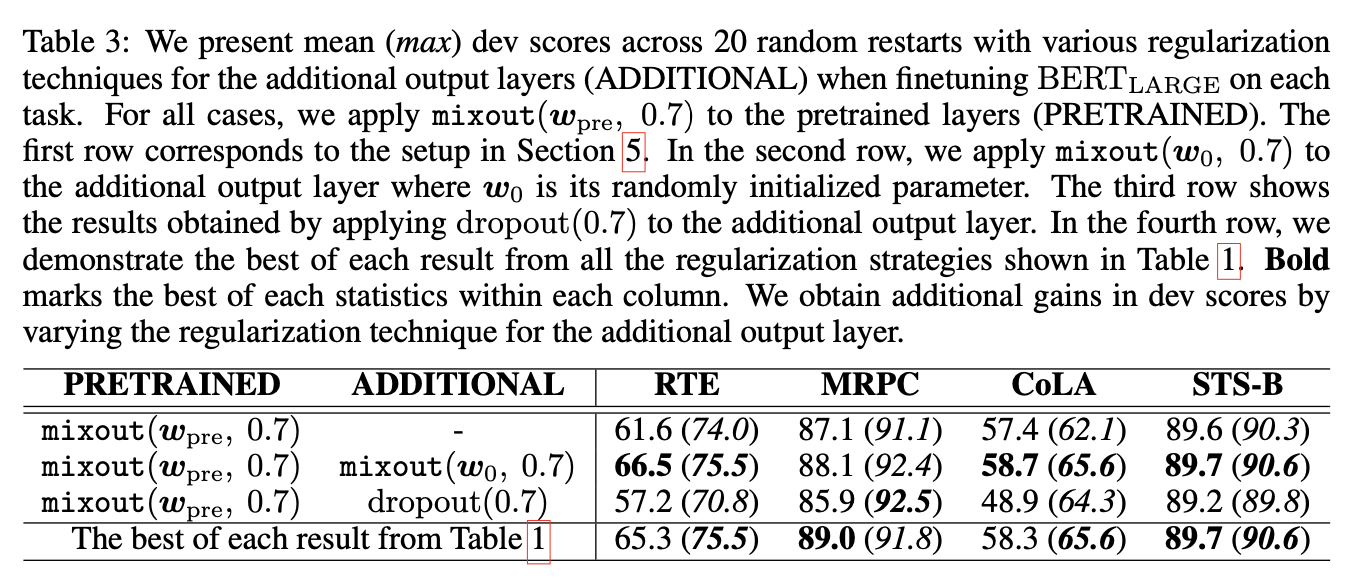
Effect of Mix Probability for Mixout and Dropout

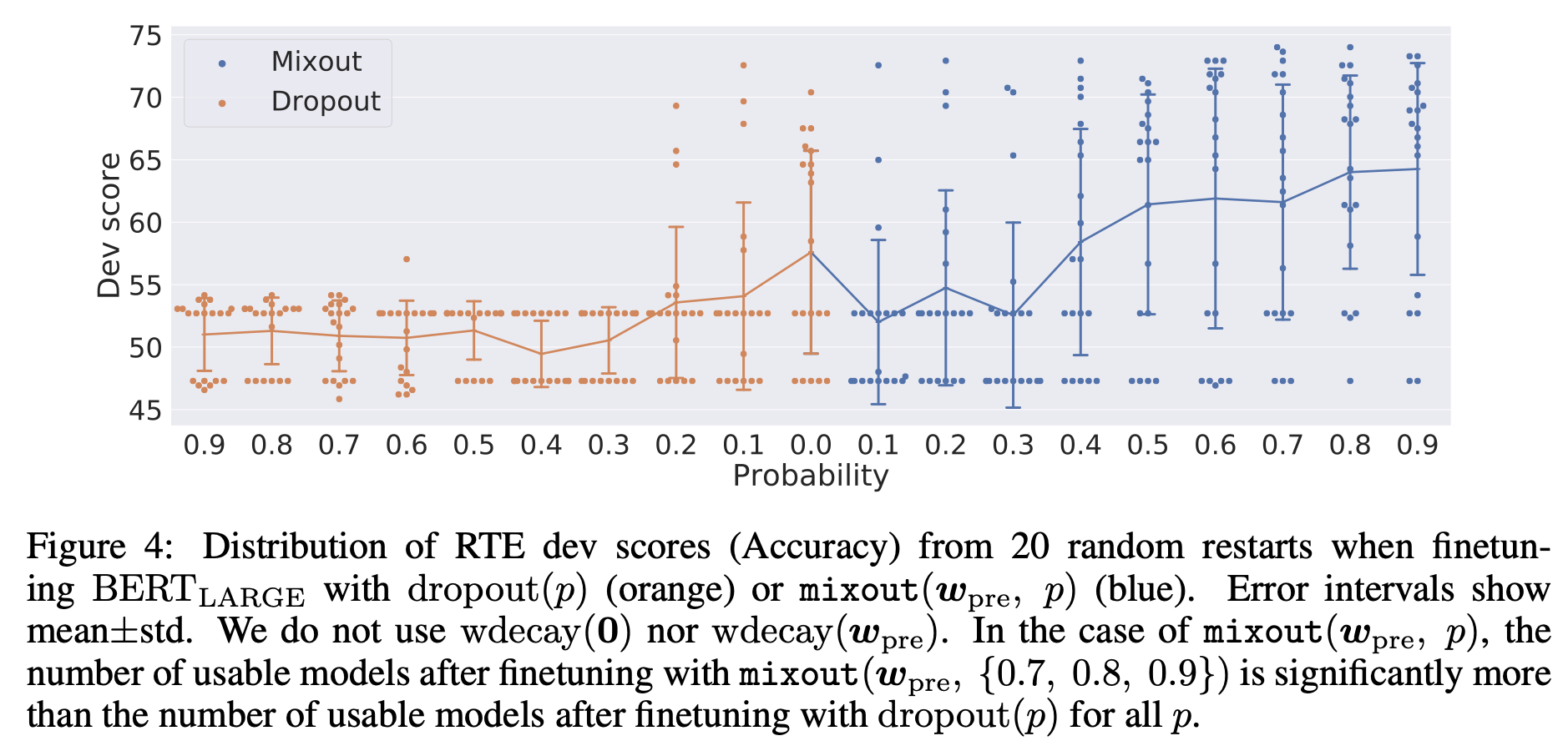
• Mixout with probability 0.7, 0.8, and 0.9 yields better average dev scores, and reduces the number of failed finetuning runs.
• But finetuning using mixout takes more time than dropout. (843 seconds vs 636 seconds)