이 논문에서는 BERT, RoBERTa가 매우 좋은 성능을 보이지만, memory, computing power가 너무 많이 필요하므로 그를 압축해보는 방법을 제안한다. 아직 WIP인 논문이고, https://arxiv.org/abs/2004.04037가 링크이다. 화웨이에서 나온 논문이다.

Abstract

• dynamic BERT Model 제안, width, depth 방향으로 dynamic함
• Knowledge Distillation 방식으로 full BERT 모델을 width adaptive BERT로 학습한 뒤, width, depth 모두 adaptive하게 학습함

1. Introduction

• 기존의 Transformer-based model을 압축하거나, 추론 가속화를 시도한 방법론들:
  • low-rank approximation
    • ALBERT: A Lite BERT for Self-supervised Learning of Language Representations
    • A Tensorized Transformer for Language Modeling
  • weight sharing
    • Universal transformers
    • ALBERT: A Lite BERT for Self-supervised Learning of Language Representations
  • knowledge distillation
    • Distilbert, a distilled version of bert: smaller, faster, cheaper and lighter
    • Patient knowledge distillation for bert model compression
    • Tinybert: Distilling bert for natural language understanding
  • quantization
    • Efficient 8-Bit Quantization of Transformer Neural Machine Language Translation Model
    • Q8bert: Quantized 8bit bert
    • Q-bert: Hessian based ultra low precision quantization of bert
  • pruning
    • Pruning Convolutional Neural Networks for Resource Efficient Inference
    • Pruning a BERT-based Question Answering Model
    • Are sixteen heads really better than one?
    • Analyzing Multi-Head Self-Attention: Specialized Heads Do the Heavy Lifting, the Rest Can Be Pruned
    • Fine-tune BERT with sparse self-attention mechanism
• 몇몇 리서치에서 depth adaptive models도 충분한 의미가 있음을 증명
• 최근의 리서치는 width direction도 충분히 redundant함을 말하고 있음
  • ex> Attention Head를 pruning해도 충분히 성능이 좋음
• CNN에서 width, depth - adaptive하게 모델을 만들어낸 시도가 있었지만, BERT에 적용하긴 힘들다.
  • Transformer 레이어 안의 Multi Head Attention과 Position wise Feed Forward Network 때문
• Training 방법
  • width adaptive BERT 학습 : attention heads랑 neuron 중 중요한 것들만 rewire한 뒤 distillation 진행
  • adaptive BERT 학습 : width adaptive BERT에서 initialize한 뒤에 width, depth 둘 다 distillation

2. Related Work

2.1. Transformer Layer

이거는 그냥 Transformer 설명임

2.2. Compression for Transformer/BERT

• Low Rank Approximation
  • weight matrix를 두 lower rank matrix의 곱으로 근사한다.
  • ALBERT는 embedding layer를 근사
  • Tensorized Transformer는 MHA 결과가 orthonormal base vectors로 표현 가능하다고 함 + multi-linear attention 사용
• weight sharing
  • Universal Transformer는 layer간 weight sharing
  • Deep Equilibrium Model은 특정 레이어의 input, output이 같아지게 함 -> ??? 모르겠다 찾아보자
  • ALBERT는 레이어간 parameter sharing이 network parameter를 안정적으로 만들게 해주고 좋은 성능을 얻는다고 함
  • 근데 model size는 줄어도 inference는 안빠름
• Distillation
  • DistilBert는 soft logit이랑 hidden states distillation 시킴
  • BERT PKD는 intermediate layer에 로스 줌
  • Tiny BERT는 general distillation, task-specific distillation으로 나눠서 진행함
• Quantizaiton
  • QBERT는 second order information을 활용해 각 레이어별로 몇 비트를 할당할 지 정함
    • steeper curvature에는 더 많은 bit 할당
  • Fully Quantized Transformer는 uniform min max quantization을 씀
  • Q8BERT는 quantization aware training + symmetric 8 bit linear quantizatio 활용함
• Pruing
  • “Fine-tune BERT with sparse self-attention mechanism”이란 논문에서 sparse self attention을 사용
  • “Compressing bert: Studying the effects of weight pruning on transfer learning”이란 논문에서 magnitude-based pruning 사용
  • LayerDrop에서는 transformer layer들의 추론을 위해 structed dropout을 적용함
• 근데 이 방법들 대부분이 압축과 관련된 거고 Universal Transformer나 LayerDrop, Depth-adaptive transformer도 압축이랑 가속에 신경쓰기는 하나 depth direction뿐이다.

3. Method

3.1. Training DynaBERT_w with Adaptive Width

• CNN과 비교해 BERT는 Transformers Layer가 쌓여있는 형태라 더 복잡
• MHA에는 linear transformation과 key, query, value의 곱이 존재함.

3.1.1. Using Attention heads and Intermediate Neurons in FFN to Adapt the Width

• MHA를 각 Attention 연산으로 분리한 다음 중요한 attention heads만을 취한다.
• 가장 중요한 순으로 Head와 Neuron을 왼쪽으로 몰아넣는다.

3.1.2. Network Rewiring

• “Pruning convolutional neural networks for resource efficient inference”와 “Analyzing multi-head self-attention: Specialized heads do the heavy lifting, the rest can be pruned” 에 따라서 importance score를 구함.
• 그런 다음 아래처럼 재구성함

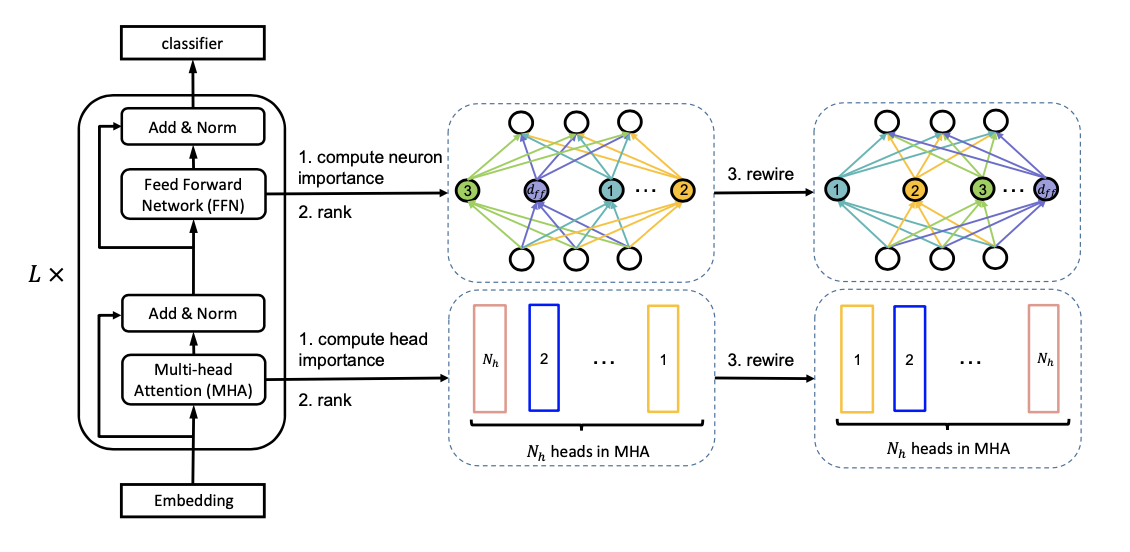
3.1.3. Training with Adaptive Width

• distillation은 logits, embedding, hidden states를 비교한다. 각각은 아래처럼 로스를 계산
  • \[l_{pred} (y^\prime, y) = - \text{softmax} (y) \text{log_softmax} (y ^\prime)\]
  • \[l_{emb}(E^\prime, E) = MSE(E^\prime, E)\]
  • \[l_{hidn}(H^\prime, H) = \sum^L_{l=1} MSE(H^\prime_l, H_l)\]
• 그렇게 구한다음 각각에 weight를 주어서 더한다.
• data augmentation이 적용되어 있다.

3.2. Training DynaBERT with Adaptive Width and Depth

• 그 다음 depth 방향으로 distillation한다.
• width direction으로 학습한 것의 catastrophic forgetting을 막기 위해 아래처럼 학습한다.

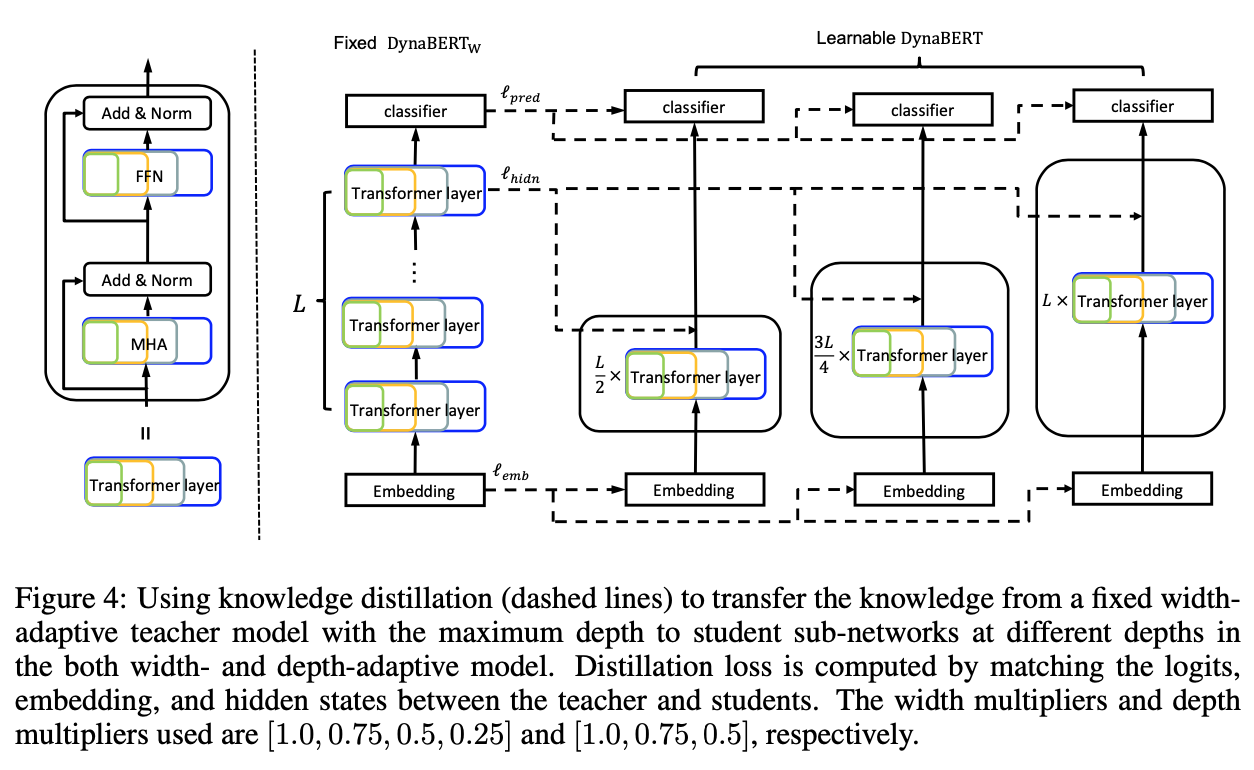
• depth layer에서는 \(mod(d + 1, \frac 1 {m_d}) = 0\)인 레이어를 drop 했다.
  • ex> 0.75를 depth multiplier로 가져가면 Bert base 기준으로 3,7, 11을 drop한다.
  • 마지막 레이어를 취하기 위함이라고 한다.
• loss는 wide adpative와 같이 가져가는데 각 loss별 weight가 다르다.

• 그리고 마지막에 fine-tuning도 할 수 있는데, 이건 predicted label이랑 ground-truth label을 cross entropy로 fine tuning한다.

4. Experiment

• BERT base, RoBERTa base와 비교
• 몇몇 하이퍼 파라미터
  • Layer = 12
  • hidden size = 768
  • intermediate size = 3072
  • width multipliers = 1, 0.75, 0.5, 0.25
  • depth multipliers = 1, 0.75, 0.5
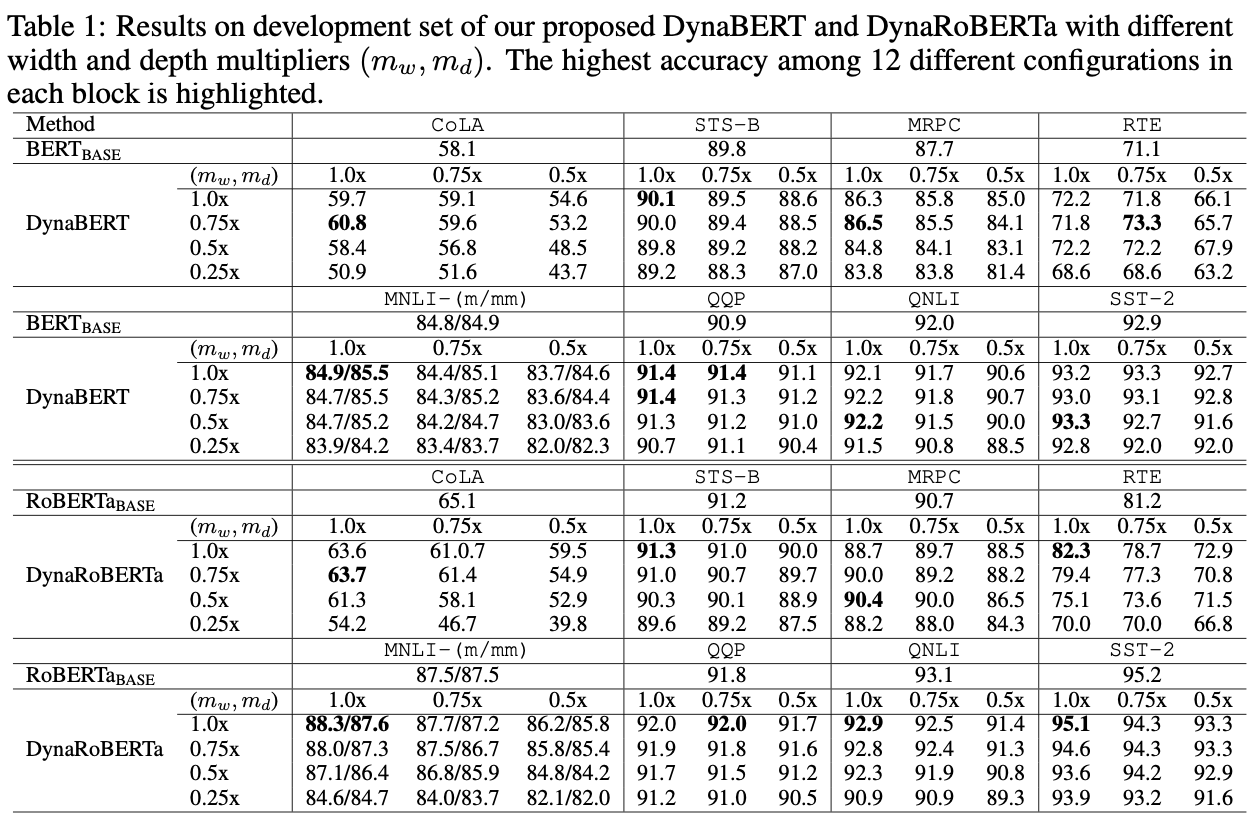
• 일단 뭐 BERT, RoBERTa base에 비해 데이터를 더 넣고 학습을 더 한 것이니 multiplier가 1, 1인 경우에는 당연히 더 잘나온다.
  • 그래도 주목할만한 점은 생각보다 그렇게 성능이 떨어지지 않는다는 점
  • ex> CoLA의 경우 BERT base가 51.5를 기록하는데, DynaBERT의 depth 0.75, width 0.25가 51.6을 기록한다. (단순 acc 비교)

• 아래는 FLOPs를 비교한 그래프이고, 더 자세한 차이를 볼 수 있다.
  • 상당히 많이 차이나는 FLOPs로 엇비슷한 성능을 낼 수 있다.

4.3. Ablation Study

• Adaptive Width
  • 그냥 BERT, network rewiring없이 학습한 DynaBERT, network rewiring한 DynaBERT, Distillation + Data Augmentation까지한 DynaBERT를 각각 Finetuning함
  • 당연히 rewiring + distillation + data aug한 것이 제일 잘 나오고, 생각보다 network rewiring이 큰 영향을 준다.
  • 아쉬운 점은 data augmentation도 따로 해줬으면…
• adaptive width and depth
  • 그냥 Vanilla DynaBERT와 Distillation + Data aug한 DynaBERT, Fine-Tuning한 것을 비교함
  • 당연히 fine tuning + distailltion + Data aug한 것이 잘 나온다.
  • 생각보다 그 폭이 큰 것도 있고, 하지만 fine tuning 안 한것이 더 잘나오는 태스크도 있다 (MRPC)

5. Discussion

5.1. Comparison of Conventional Distillation and Inplace Distillation

• 해봤는데, 음… 어.. 한 수준이다. 잘 나오는 것보다 있고, 아닌 것도 있지만 그저 그런 수준.

5.2. Different Methods to Train DynaBERT_w

• Progressive rewiring
  • 계속 진행해가면서 낮은 width multiplier를 추가하는 방식인데, 너무 오래 걸리는 방법이다.
  • 별로 성능 이득 없다
• Universally Slimmable Training
  • 매 iteration마다 여러 width multipliers를 골라놓고 학습한다.
  • 별로 큰 차이 없다.

6. Conclusion and Future Work

• 나중에는 hidden size도 바꿀 수 있도록 해볼 것
• 아니면 ALBERT처럼 weight sharing하는 방법?
• pretraining stage에도?