• CS224W
• Youtube link

introduction

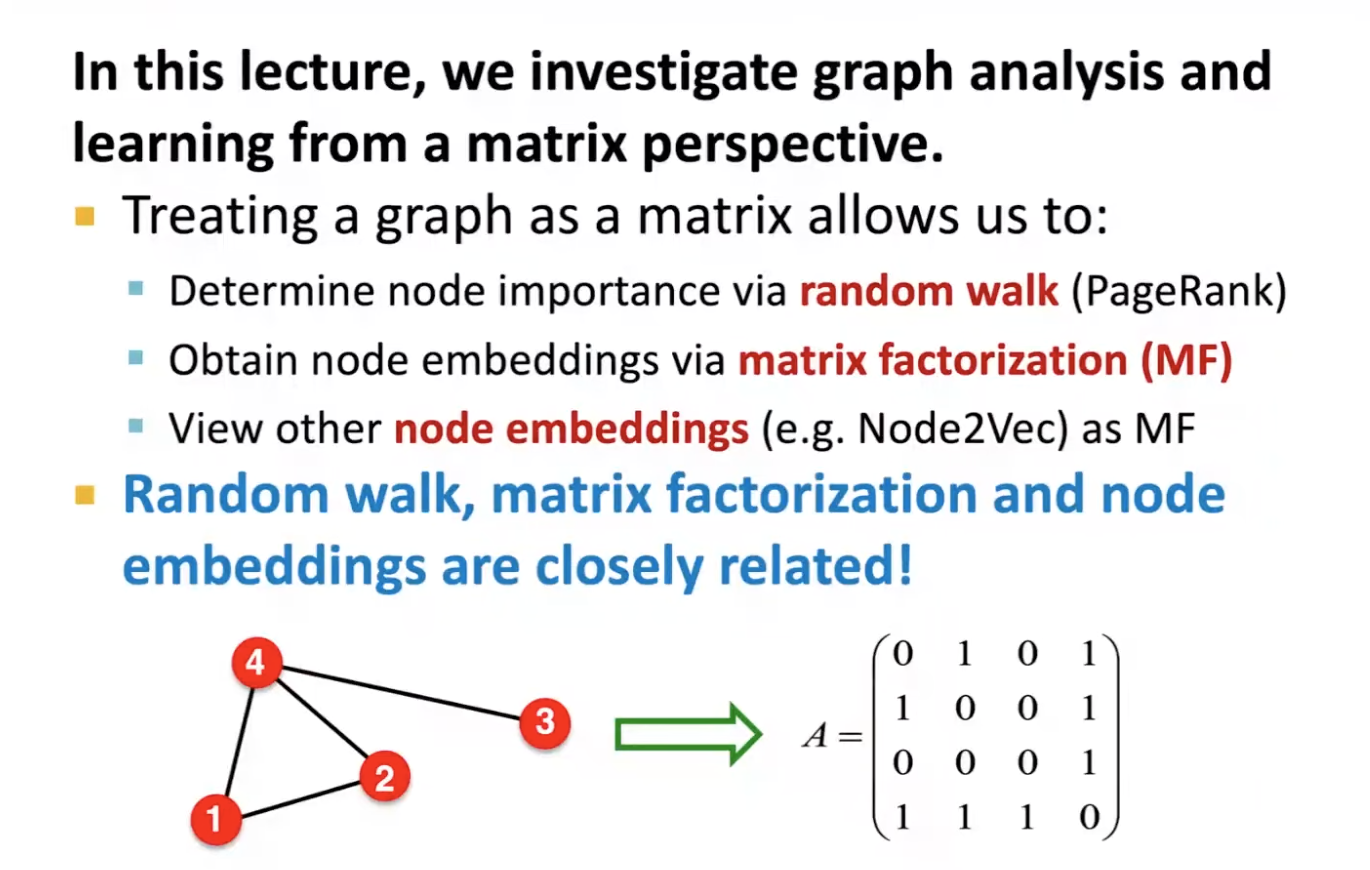
• the web as a graph
  • nodes: webpage, edges: hyperlinks
  • directed graph
  • all nodes are not equally important
  • => rank the pages using link structure
• link analysis algorithm (to compute importance of nodes)
  • page rank
  • personalized page rank (PRR)
  • random walk with restarts

PageRank

• Links as votes
• => page rank
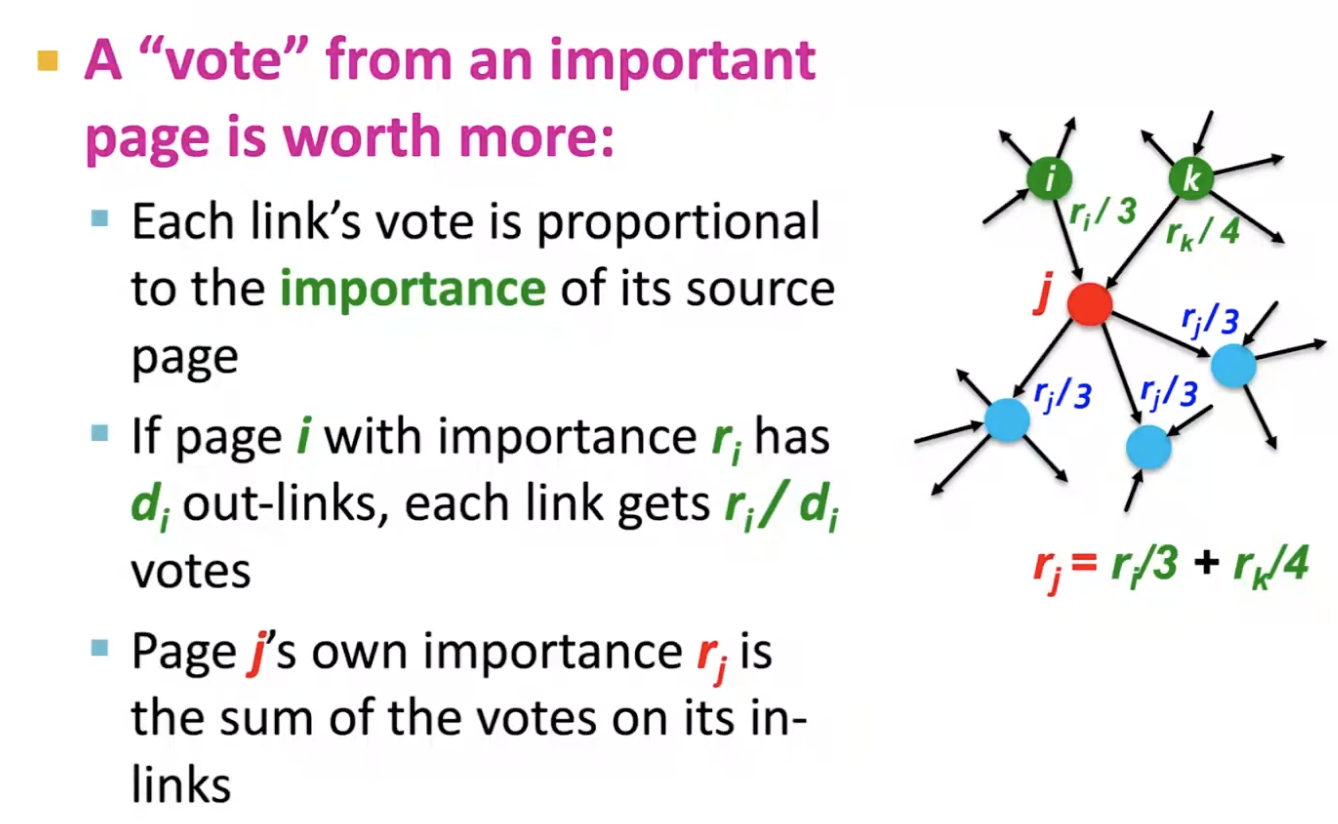
  • long term distribution of the surfers
  • page rank: pincipal eigenvector of stochastic adjacency matrix
    • we can efficiently solve with power iteration.
• page rank summary

• how to solve pagerank

  • problem:
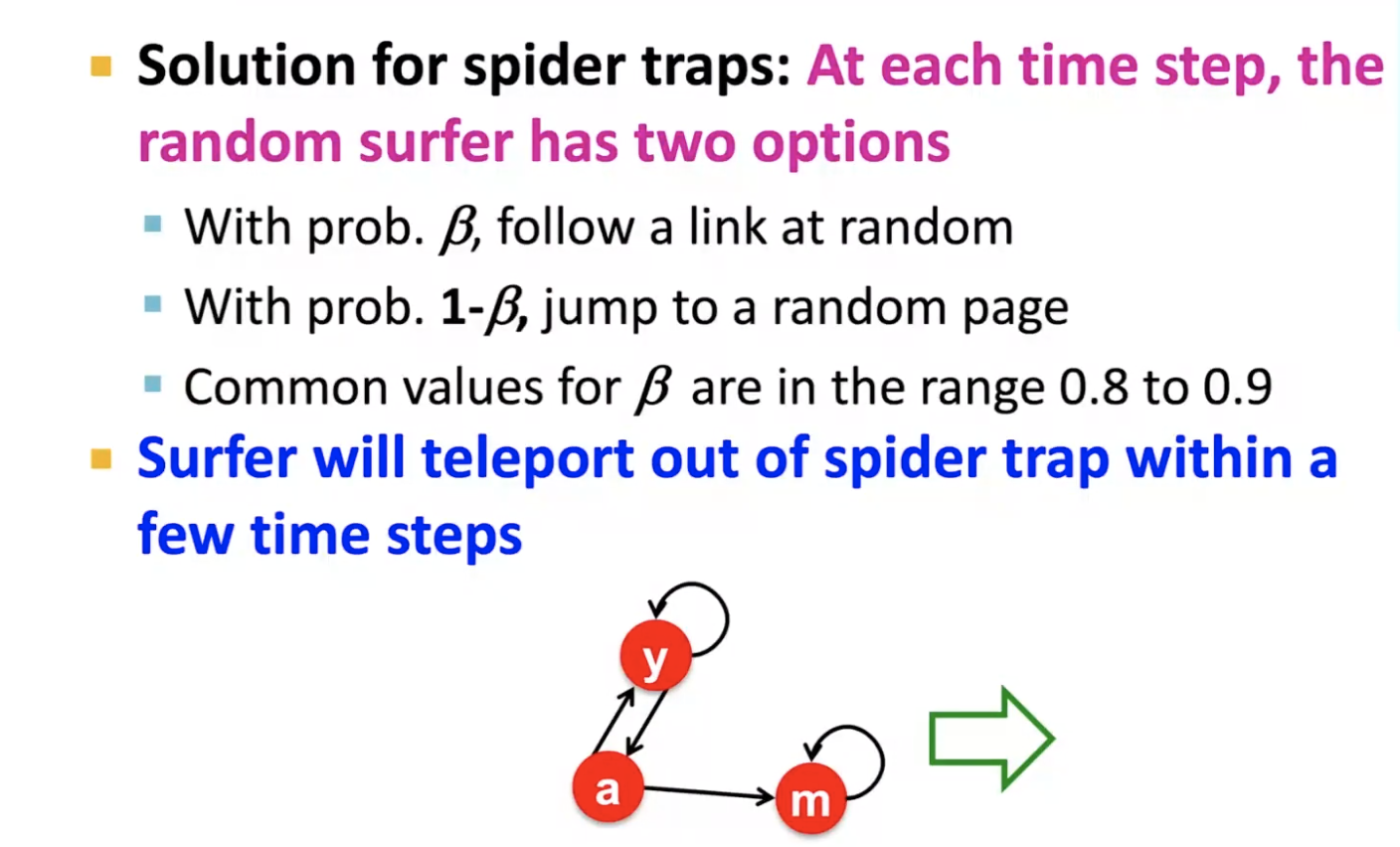
    • spider trap (all out links are within the group)
      • spider traps are not a problem, but with traps, page rank scores are not what we want
      • solution: random jump (or teleport)
    • some pages are dead ends (no out link)
      • dead ends are a problem
      • solution: 100% teleport

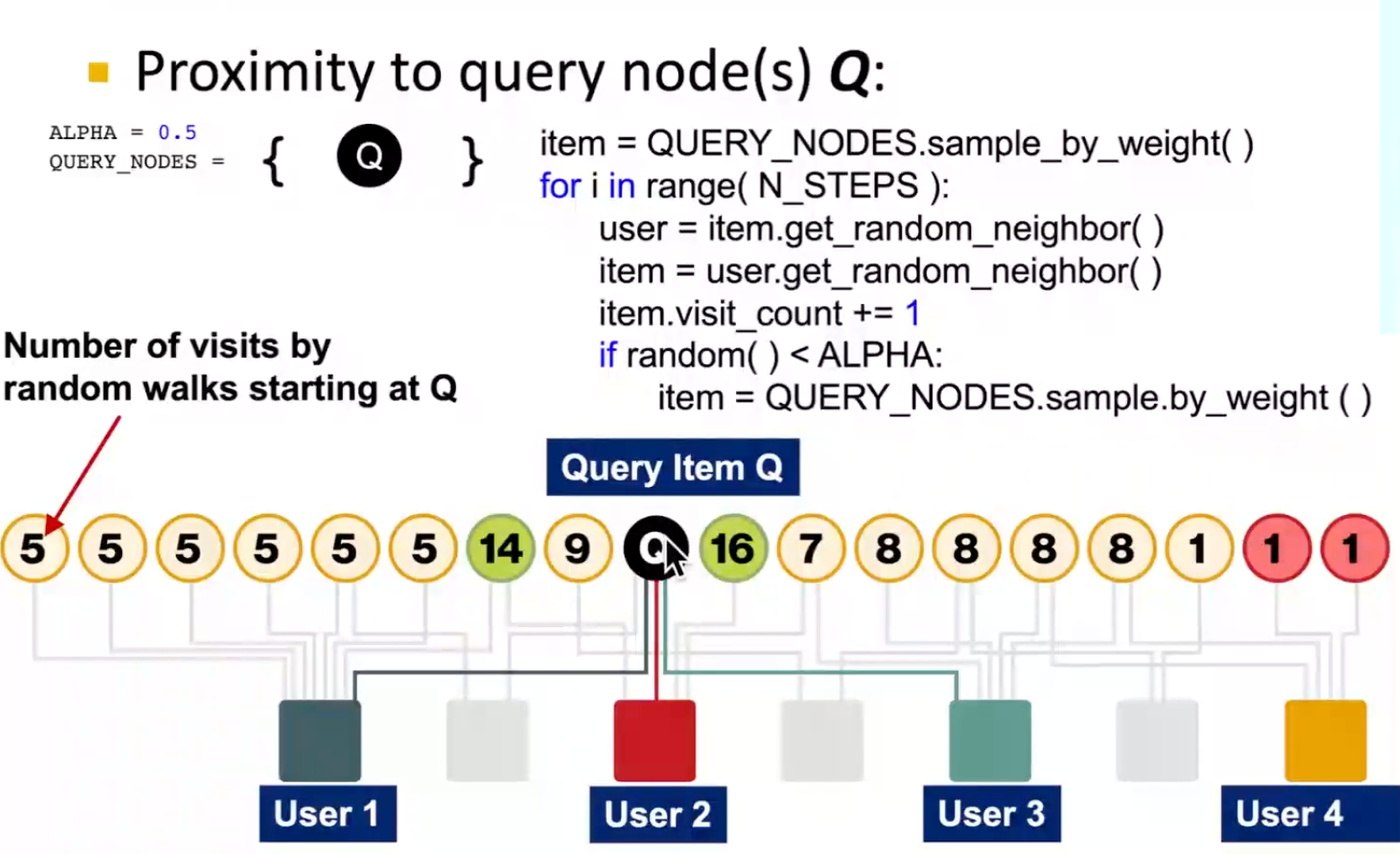
Random Walk with Restarts and Personalized PageRank

Matrix Factorization and Node Embeddings

• simplest approach -> embedding lookup
• =>
• limitation:
  • cannot obtain embeddings for nodes not in the trainset
  • cannot capture structural similarity
  • cannot utilize node, edge, and graph features