• CS224W
• Youtube link

Introduction

• traditional ml for graphs
  • input-graph => feature-engineering => structured feature => learning algorithm => prediction
• graph representation learning
  • input-graph => feature-engineering representation learning => structured feature => learning algorithm => prediction
  • goal: efficient task-independent feature learning
  • task: map nodes into an embedding space
    • possible downstream tasks: node classification, link prediction, graph classification, anomalous node detection, clustering, …

node embeddings: encoder and decoder

• encoder: maps from nodes -> embeddings
• decoder(similarity function): maps embeddings -> similarity scores
• learning node embeddings: optimize parameters of the encoder
• simplest approach: encoder is just an embedding-lookup (DeepWalk, node2vec)
• deep encoders -> lecture 6
• objective: maximize similarity score for node pairs that are similar
• key choice: how can we define node similarity

random walk approaches for node embeddings

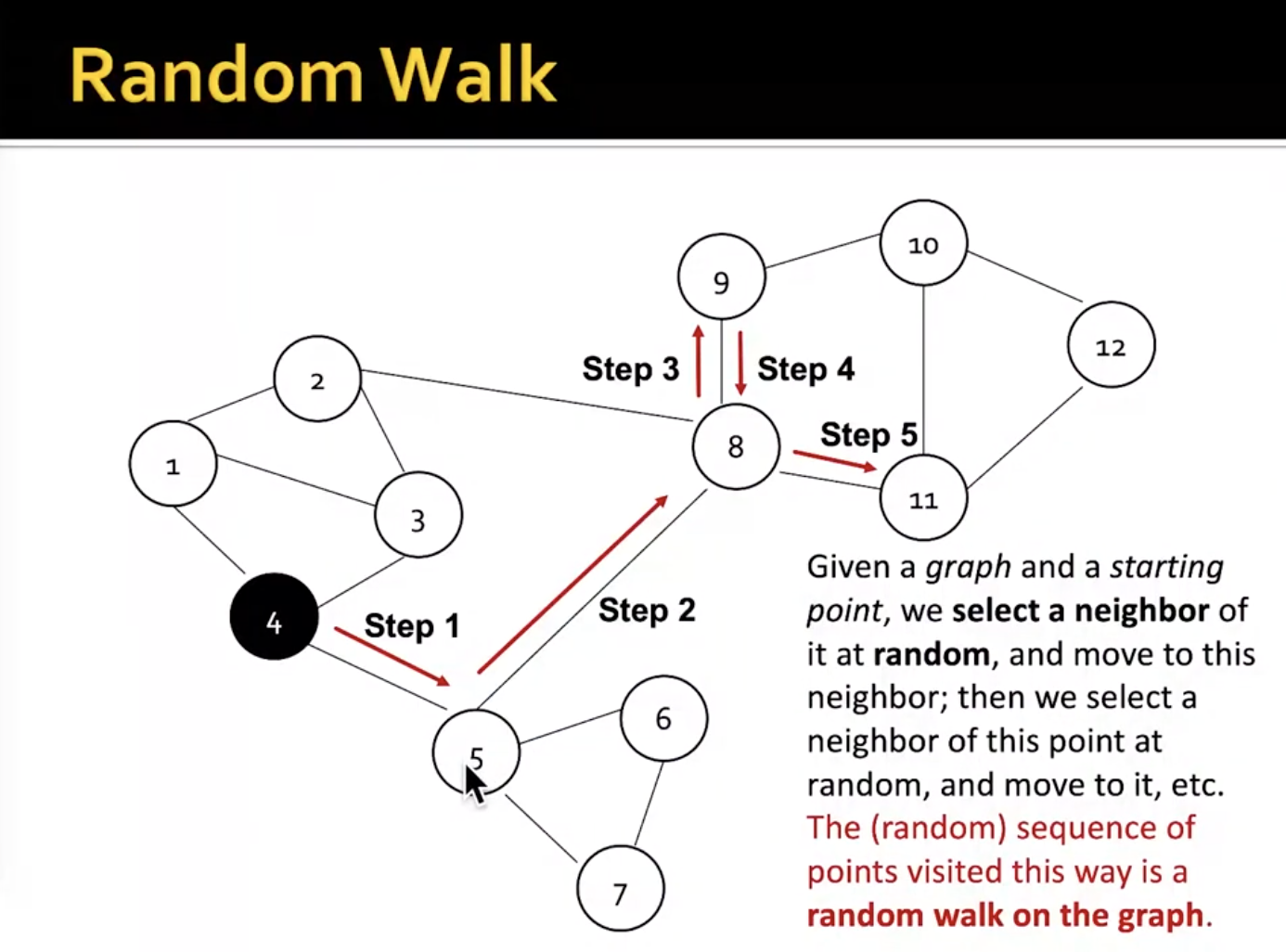
• similarity score approximates a probability that two nodes co-occur on a random walk over the graph

• why random walk?

  • random walk optimization is computationally expensive => use negative sampling
  • how to solve optimization problem? => SGD
• strategy to walk randomly
  • simplest: just fixed-length, unbiased random walk -> DeepWalk
  • issue: similarity is too constrained
  • how can we generalize this? -> node2vec

Node2Vec

• goal: embed nodes with similar network neighborhoods close in the feature space

• key observation: flexible notion of network neighborhood leads to rich node embeddings

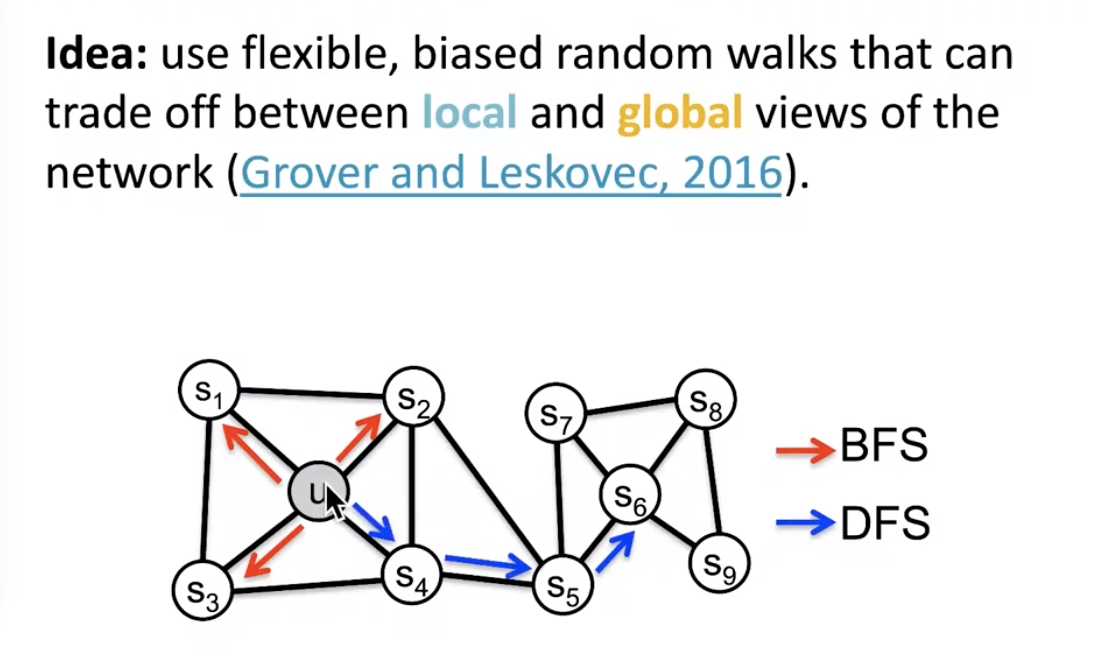
  • BFS strategy can capture local features
  • DFS strategy can capture global features
• hyperparameter for node2vec
  • p: return back to the previous node
  • q: in-out parameter, ratio of BFS vs DFS
• biased 2nd-order random walks
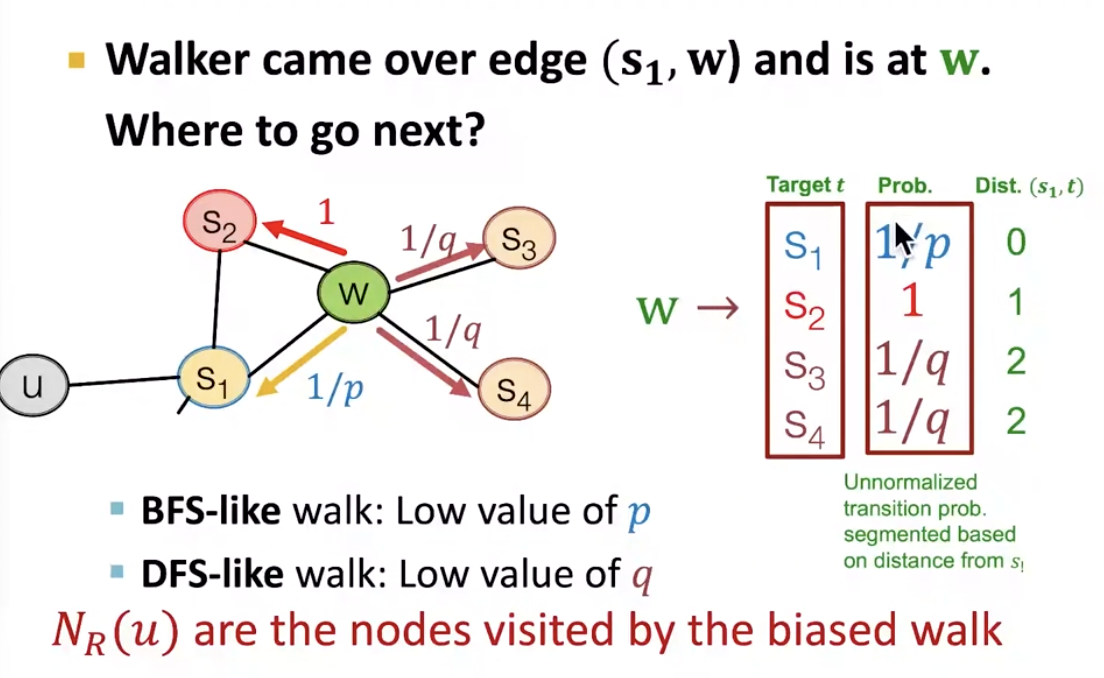
  • idea: remember where the walk came from

• node2vec algorithm

  1. compute random walk prob
  2. simulate random walks of specific length starting from each node
  3. optimize the node2vec objective using SGD

embedding entire graphs

• goal: embed subgraph or entire graph
• approaches
  • (simplest) average the node embeddings
  • add virtual node to represent (sub)graph and run standard graph embedding technique

  • anonymous walk embeddings

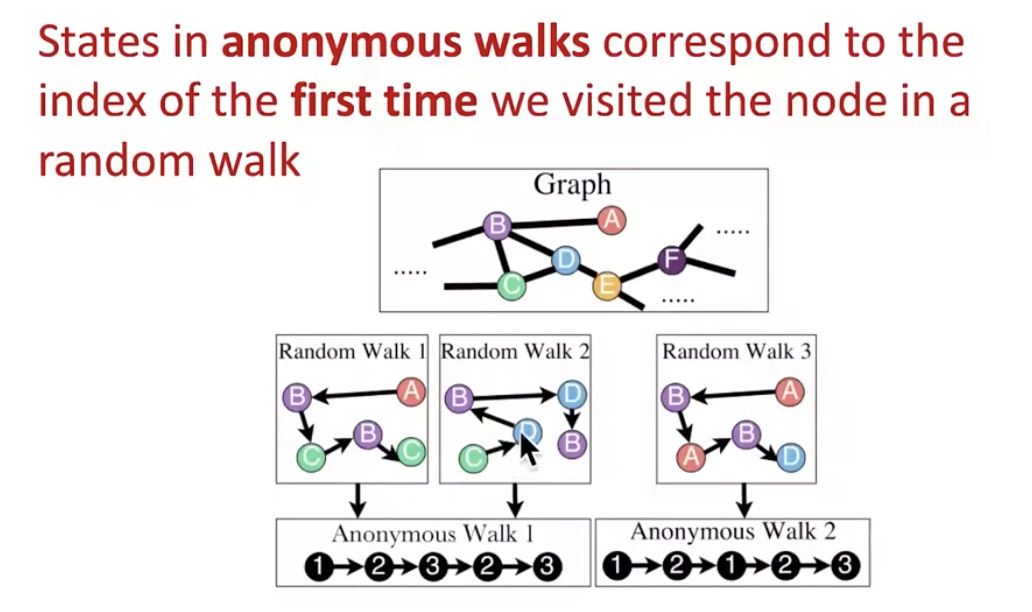
    • sample use of anonymous walk
  • learn walk embeddings of anonymous walk
  • hierarchiccal embeddings -> later in this lecture
    • we can hierarchically cluster nodes in graphs, and sum/avg the node embeddings