CS224W Lecture 2 Traditional feature based methods
- This lecture
- In traditional graph ml pipeline, features for nodes, link, and graphs are manullay desinged. (hand-designed features)
- topic of this lecture: traditional features for ..
- node level preiction
- link level prediction
- graph level prediction
- for simplicity, we focus on undirected graphs
- Node level tasks
- features
- node degress
- the number of edges the node has
- nothing special, but very useful feature
- node centrality
- node degree counts the neighboring nodes without capturing importance.
- different ways to model importance
- eigenvector centrality
- betweenness centrality
- closeness centrality
- and many others…
- clustering coefficient
- graphlets
- clustering coefficient counts the # triangles in the ego-networks
- => so we can generalize it by counting # pre-specificed subgraphs
- graphlet degree vector (GDV): graphlet-base features for nodes
- degree counts # edges that a node touches
- clustering coefficient counts # triangles that a node touches
- GDV counts # graphlets that a node touches
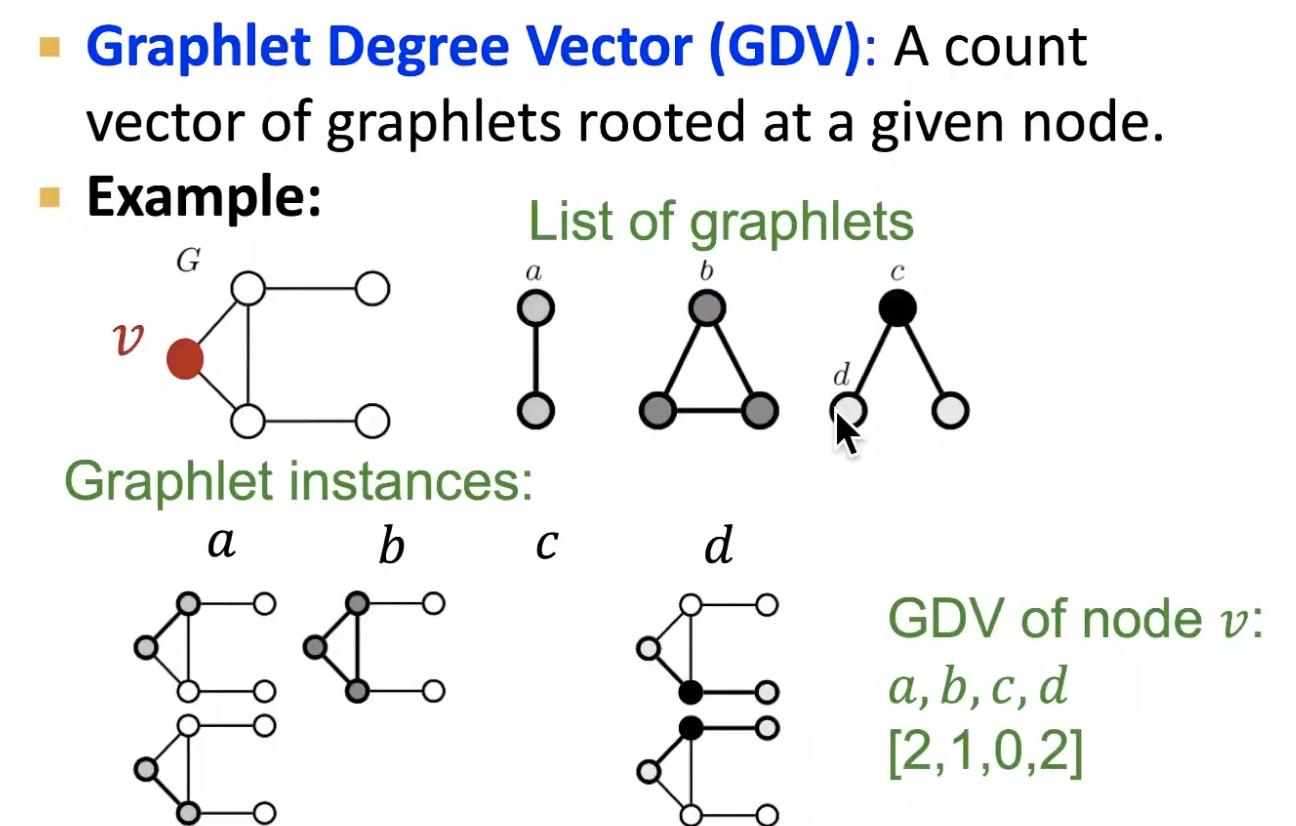
- graphlet degress vector provides a measure of a node’s local network topology
- node degress
- features
- Link level tasks
- link level prediction task: the key is to design features for a pair of nodes
- link level features:
- distance based feature => shortest path distance between two nodes.
- this does not capture the degree of neighborhood overlap
- local neighborhood overlap
- captures # neighboring nodes shared between two nodes
- but this is always zero if the two nodes don’t have any neighbors in common
- global neighborhood overlap
- katz index: count the number of paths of all lengths between a given pair of nodes -> via powers of the graph adjacency matrix

- distance based feature => shortest path distance between two nodes.
- Graph level tasks
- kernel method
- idea: design kernels instead of feature vectors
- kernel \(K(G, G')\) measures similarity between data
- there exists a feature representation \(\phi\) such that \(K(G, G') = \phi(G)^T\phi(G')\)
- graph kernel
- key idea: bag of words for a graph
- below kernels use Bag-of-* representation of graph
- graphlet kernel
- count the number of different graphlets in a graph
- we can normalize graphlet kernel features if graphs to compare have different sizes.
- but graphlet kernel is expensive operation.
- Weisfeiler-Lehman Kernel
- idea: use neighborhood structure to iteratively enrich node vocabulary
- generalized version of bag of node degress since node degrees are one-hop neighborhood info.
- color refinement: algorithm for Weisfeiler-Lehman Kernel
- after calculating color refinement, WL kernel counts number of nodes with a given color
- this method is computationally efficient
- other kernels
- random walk
- shortest path graph kernel
- ..
- kernel method
November 8, 2021
Tags:
cs224w