저번주부터 CS224n 스터디를 시작했다! CS231n 들을 때랑 다르게 다른 사람이랑 같이 하면 그래도 끝까지 듣지 않을까 싶어서 한번 해보자고 주위사람들을 끌어모아봤다. 이 포스트는 1강 강의 노트를 정리한 포스트이다.

Introduction

간략하게 가르칠 것에 대한 내용을 설명한다.

• NLP with Deep Learning
• 인간의 언어를 이해하는 것에 대한 빅 픽쳐 (인사이트..?)
• pytorch로 진짜로 구현해보기
  • word meaning
  • dependency parsing
  • machine translation
  • quesion answering 등등등…

이번부터 pytorch를 사용한다고 한다.

Word Vectors

Human Language and word meaning

language란 것 자체가 상당히 불확실한 것이다. 정보를 전달하는 수단이기도 하며 socialize하는 수단(사람들이 네트워킹 하는 수단)이기도 하다. 그런 언어를 컴퓨터로 분석하는 것은 computer vision 등에 비하면 상당히 최근의 일이다. 그래도 일단 알고 가야할것은 다른 정보 교환 수단에 비해서 언어를 통해서 정보를 주고 받는 것은 상당히 속도가 느리다.

그럼 언어/단어를 통해 전달하는 meaning의 뜻 무엇일까. “word, phrase등으로 표현하고자 하는 무언가”이다. 그래서 일반적으로 meaning을 표현하는 방법은 signifier(symbol) <=> signified(idea or thing) 정도이다.

근데 그럼 meaning을 컴퓨터로는 어떻게 사용하고, 이해해볼 수 있을까. 간단하게 wordnet를 사용해볼 수 있겠다. 유의어 등을 수많이 정리해놓은 사전과 유사한 리스트이다. (nltk안에 포함되어 있다)

• 그럼 이 wordnet을 사용한다고 좋을까? 문제점은 없을까?
  • 뉘앙스가 없어진다.
  • 새로운 단어들이 없다.
  • 주관적이다.
  • 인간의 노동이 다소 많.....이 들어간다.
  • 단어의 유사도를 정확히 표현할 수 없다.

그래서 neural net 스타일로 나타내기 시작했다. (Representing words as discrete symbols) 단어를 벡터로 나타내자! 그래서 하나하나의 단어를 one-hot 벡터로 나타내는데, 문제

• 단어의 수가 너무 많다.
• 그리고 모든 벡터가 orthogonal하다. (one-hot 벡터니까..)
• 벡터로 나타냈는데 유사도따위 버렸다.

그래서 유사도를 벡터 자체가 포함할 수 있도록 encoding하자! 이러한 생각에 대해 아주 큰 인사이트를 J. R. Firth란 사람이 주었는데, 이는

Distributional semantics: A word’s meaning is given by the words that frequently appear close-by

이다. 비슷한 단어는 비슷한 위치에 많이 위치한다. 그래서 단어의 의미를 context로부터 뽑아온다. 즉 단어를 context를 사용해 embedding하여 dense vector로 표현한다. 학습 후 n dimension을 visualize해보니까(PCA 등으로) 비슷한 단어가 다 모여있더라.

word2vec overview

word2vec의 메인 아이디어는 이거다.

• 큰 corpus의 데이터 안에서 모든 단어를 vector로 표현하자.
• word vector의 유사도를 이용해 해당 단어가 해당 context에 있을 확률을 계산하자.
• 계속 확률을 maximize하기 위해 word vector를 조절하자.

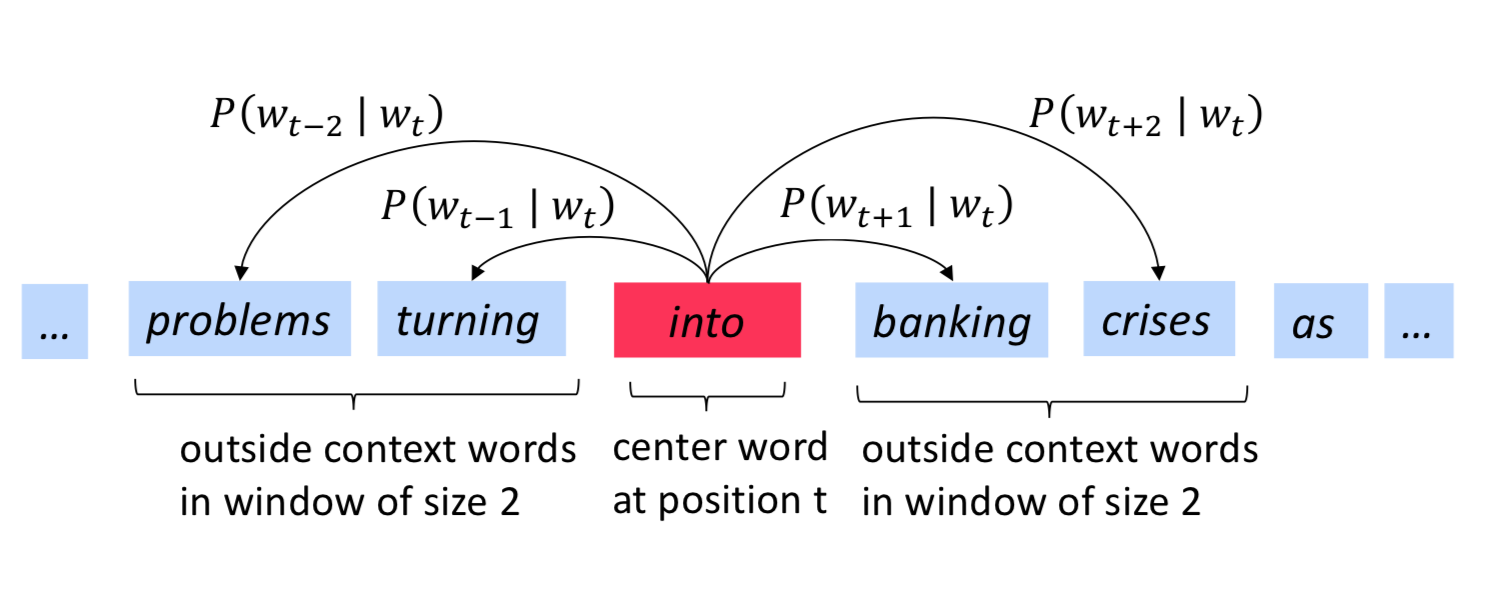
자 그럼 실제로 자세하게 살펴보자. objective function (cost, error function)으로는 아래 함수를 사용한다.(\(J(\theta)\)) \(T\)는 전체 단어의 갯수이다. \(t\)는 단어의 position이다. \(m\)은 window size이다.

\[L(\theta) = \prod_{t=1}^T \prod_{-m \leq j \leq m, j \neq 0} P(w_{t + j} | w_t; \theta)\] \[J(\theta) = - \frac 1 T log L(\theta)\]

\(\theta\)가 optimize될 변수이고, \(L\)은 likelyhood, 우도를 가리키며, 때때로 \(L = J'\)이다. objective function을 minimize 시키는 것이 predictive accuracy를 maximize하는 것이 된다.

자 그럼 확률은 어떻게 계산하냐면, 일단 먼저 \(\vec u\)와 \(\vec v\)를 먼저 정의한다.

• \(\vec u_w\)는 단어가 context word일때 쓰는 벡터이다.
• \(\vec v_w\)는 단어가 center word일때 쓰는 벡터이다.

그떄 center word가 c이고, context word가 o일떄 확률을 아래처럼 계산한다.

\[P(o|c) = \frac {exp(u_o^T v_c)} {\sum_{w\in V} exp(u_w^T v_c)}\]

softmax 식과 비슷하다. 여담으로 softmax의 soft는 확률이라 soft하게 분포시킨다는 말이고, softmax의 max는 제일 확률을 증폭시킨다는 말이다.

Optimization

여튼 이렇게 식들을 정했으니 학습을 위해서는 optimization을 해야한다. \(\theta\)는 \(2dV\)의 차원이 되고, (V개의 단어에 대해 d차원의 벡터들이 2개씩(u, v) 있다) 그냥 \(\theta\)를 바꾸면서 \(J\)를 minimize시키면 된다고 한다. 편미분 하는 건 나중에 다시 봐도 알거라 생각하고.. 적어보면 아래와 같다.

\(J(\theta) = - \frac 1 T log L(\theta)\) 이고, \(L\)이 \(\prod\)를 포함하니까 로그가 \(\prod\)안으로 들어가면서 \(\prod\)가 \(\sum\)으로 바뀐다. 그 때

\[\frac \partial {\partial v_c} log p(o | c) = u_o - \sum_{x=1}^V p(x|c) u_x\]

이다. \(u_o\)가 실제 context word이고, 그 뒤의 항이 expected context word이다. 즉, 실제 context word와 expected context word의 차이를 줄인다.

여튼 실제로 구현할 때 numpy, matplotlib, jupyter, gensum, sklearn을 참고해서 구현하는데, 그냥 colab으로 하면 될 거 같다.