cs224n 스터디를 하면서 나오는 과제들도 같이 하기로 헀다. 그래서 1, 2주차 과제를 몰아서 해봤다. 과제를 하면서 내가 다시 봐야할 내용같은 것을 적어놓았다.

1주차 과제

Question 1에서 Word Vector를 간단하게 써보고, Question 2에서 gensim으로 간단하게 analogy등을 해보는 과제였다. 전체의 소스코드는 jupyter notebook으로 제공되었고, 비어있는 일부 소스코드를 채우거나, 결과를 보고 설명을 써내는 과제였다.

Question 1

간단하게 설명하자면, co occurance를 잰 뒤 truncated svd(PCA라고 생각하면 된다)와 matplotlib을 이용하여 몇몇 단어들을 하는 것이다.

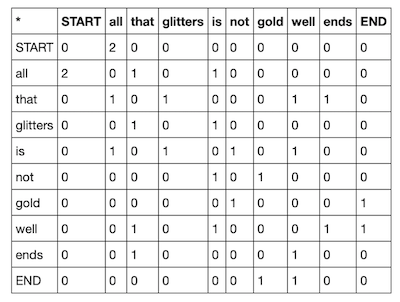
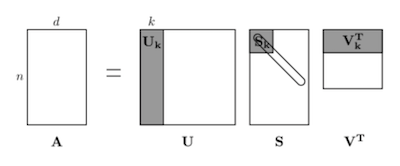
위의 내용과 아래의 내용을 참고하면 좋다고 한다.

• Computation Broadcasting

결국 그 정보를 이용해서 plotting 하면 아래같은 결과가 나온다. 나라 이름들은 상당히 많이 모여있는 모습이다.

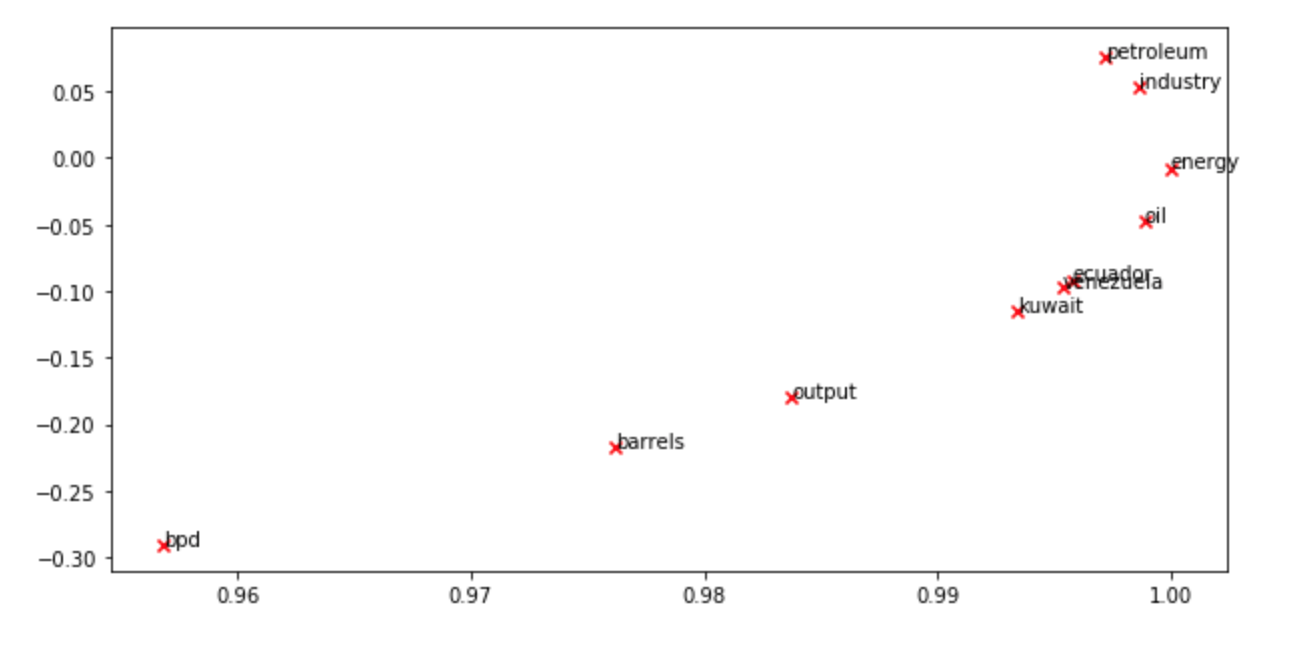
Question 2

prediction-based word vectors에 관한 내용이다. 직접 구현해보는 내용은 아니고 사용해보는 내용이기 때문에 크게 볼 내용은 없고, 아래 논문만 살펴보면 될 것 같다.

• origin paper (무엇인가 했는데 negative sampling 논문)

2주차 과제

이것도 Question이 두가지가 있는데, 첫번째는 word2vec에 필요한 수식을 구해보는 단계이고, 두번째는 그 수식을 바탕으로 코드를 작성하는 단계이다.

a2 Question 1

Question 1은 이 pdf 파일을 보자. 알아두어야 할 식은 아래 정도이다. 이건 written 과제라 여기에 정리해놓는다.

\[P(O=o|C=c)= \frac {\exp (u_o^\intercal v_c)} {\sum_{w\in Vocab} \exp (u_w^\intercal v_c)}\] \[J_{naive-softmax}(v_c, o, U) = - \log P(O=o|C=c)\]

a

a는 naive-softmax loss가 cross entropy loss와 같아지는 이유를 적어라고 한다. 즉, 아래 식이 참인 이유를 말하라고 한다.

\[- \sum_{w \in Vocab} y_w \log \hat y_w = - \log \hat y_o\]

\(y\)는 실제 확률 분포이고, \(\hat y\)는 모델에서 구한 확률 분포이다. 그렇다면, \(y\)는 context word \(o\)에 해당하는 element만 1인 one-hot vector이고, 위의 식이 참이 된다.

b, c

b는 naive softmax loss식을 \(v_c\)에 대해 편미분 할 때!

\[\frac {\partial J} {\partial v_c} = - u_o + \sum_{x \in Vocab} P(x|c) u_x\]

근데 위의 식이 실제 분포와 가중치가 있는 확률 분포의 차이값을 계산하는 것인데, \(y\)가 outside word \(o\)에 대해서만 1이니 결국 그냥 가중치가 있는 실제 분포와 계산한 확률 분포의 차이와 같다.

\[\frac {\partial J} {\partial v_c} = U (\hat y - y)\]

c는 naive softmax loss식을 \(u\)에 대해 편미분 할 때! 계산하면 \(w = o\)인 경우는 아래처럼 나온다.

\[\frac {\partial J } {\partial u_o} = (\hat y_o - y_o) v_c\]

\((\hat y_o - y_o)\) 는 확률 분포의 element끼리 더하고 뺀거니까 스칼라값!

\(w \neq o\)인경우는 아래와 같다.

\[\frac {\partial J } {\partial u_w} = \hat y_w v_c\]

근데, 이게 \(y\)가 \(o\)번째 element만 1인 one-hot vector이니 결국 전체 \(U\)에 대해 편미분 하면 아래와 같아진다.

\[\frac {\partial J} {\partial U} = (\hat y - y) v_c^\intercal\]

d

sigmoid 편미분. 이건 다른 곳에도 설명이 워낙 많으니…

\[\frac {\partial \sigma} {\partial x} = \sigma (1 - \sigma)\]

e

이건 negative sample에 대한 loss의 편미분 식을 구하는 것인데, 일단 neg sample의 loss는 아래와 같다.

\[J_{neg-sample}(v_c, o, U) = - \log (\sigma (u_o^\intercal v_c)) - \sum_{k=1}^K \log (\sigma (-u_k^\intercal v_c))\]

\(K\)가 negative samples이고, \(o\)는 neg sample에 안들어있다.

이 때 각각의 미분한 결과는 아래와 같다.

\[\frac {\partial J} {\partial v_c} = - (1 - \sigma (u_o^\intercal v_c))u_o + \sum_{k = 1}^K (1 - \sigma(-u_k^\intercal v_c))u_k\]

이 경우 실제 코드로 구현할 때는 \(U\)에서 \(o\)번째를 제외하고 전부 -1을 곱해준 후 해당 matrix 전체에 대해 sigmoid를 연산해서 사용했다. 또 \(o\)번째만 \(- (1 - \sigma)\)이고 나머지는 \(1- \sigma\)인점도 미리 전체에 대해 연산해서 사용했다.

\[\frac {\partial J} {\partial u_o} = - (1 - \sigma (u_o^\intercal v_c))v_c\] \[\frac {\partial J} {\partial u_k} = \sum_{x=1}^K (1 - \sigma(-u_x^\intercal v_c))\frac {\partial u_x^\intercal v_c} {\partial u_k}\]

이게 위의 식처럼 작성한 이유는 neg sample에 여러번 들어갈 경우 그 수만큼 더해주어야 한다.

---

이게 근데 다 맞는지는 모르겠고 일단 풀어본거다. 아래 코드로 구현했을 때 잘 나왔으니 맞는 거겠지..?

a2 Question 2

구현!!!은 그렇게까지 어렵진 않고, 수학수식을 그대로 옮겨야 하는데, 거기서 헷갈렸다. 그리고 마지막 결과를 뽑아내기까지의 시간이 오래걸린다. (numpy로 실제 학습을 시켜본다)

그렇게 얻은 결과는 아래정도이다.

그렇게 결과가 잘 나온것같진 않다. 그냥저냥 뽑아본 것에 만족한다.