• 강의 영상 : 링크
• 강의 슬라이드 : 링크

1년동안 신경안쓰다가 다시 듣기 시작했는데, 그냥 이미지 가져오고 자세한 정리 포기하고, 듣고 나서 정리하기로…

_

오늘 배우는 내용 전부는 Supervised Learning.

• Loss function : 가중치 W가 얼마나 안좋은지 정량적으로 체크
• Optimization : 가장 덜 안좋은 가중치 W를 찾는 과정

Loss function

dataset을 \(\{(x_i, y_i)\}^N_{i=1}\) 이라 할 때(\(x_i\)는 입력 데이터, \(y_i\)는 정답이라 볼 수 있다), Loss를 아래처럼 볼 수 있다.

\[L = \frac 1 N \sum_i L_i (f(x_i, W), y_i)\]

함수 \(f\)의 결과값이 prediction이고, \(y_i\)가 정답이다. 그 prediction 들과 정답 사이의 Loss 들의 평균을 위에서는 Loss Function이라 적어놓았다.

Multiclass SVM Loss

맞다/아니다만을 분류하는 것이 아닌, 여러 개의 카테고리를 분류하는 Multiclass SVM 이다. svm의 loss는 아래와 같다.

\[L_i = \sum_{j \neq y_i} max(0, s_j - s_{y_i} + safety\_margin)\]

safety margin은 SVM의 특성을 이해하면 알 수 있다. 강의에서는 1로 넣어 놓았다.

강의에서 조교의 설명 상 임의의 값을 넣은 것으로 보이지만, output score에 따라 정해질 수 있다고 한다. 매우 큰 output score일 경우 단지 1의 차이는 크지 않을 수도 있고, 1에서 0 사이의 output score일 때 1의 차이는 비현실적으로 클 수도 있다.

multiclass svm loss를 hinge loss라고 부른다. 경첩모양을 가지는데,

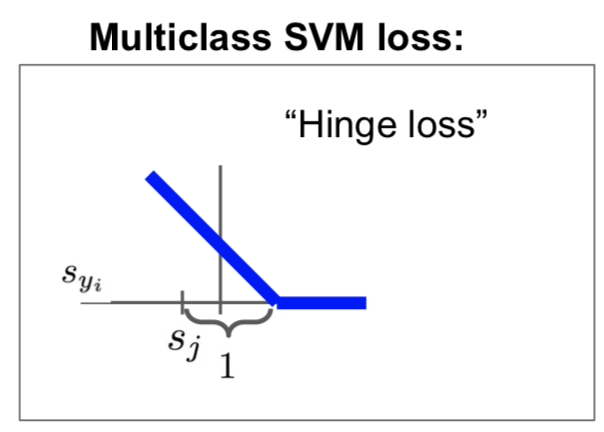
위와 같은 모양이다. 저기서는 safety margin이 1이다. 정답 class와 오답 class들의 차이가 1 이상 차이나면 신경쓰지 않는다는 의미.

Squared Hinge Loss를 쓰기도 한다는데, 이는 (max 함수)^2의 합으로 생각하면 된다. 이는 틀린 정답일 때 더 심한 loss를 주기 위해 사용한다고 한다.

여기서 위에서 말한 것처럼 합 대신 평균을 쓰면 어떻냐고 말할 수 있는데, 그것은 N값은 이미 정해져 있어서 상수값과 같으니, 단지 loss함수를 rescaling하는 것과 같다고 한다.

Regularization

분류를 간단하게 만들기 위해. (문제를 푸는 방법이 여러가지 있다면, 가장 간단한 것이 최고라고 말하는 Occam’s Razor를 찾아봐도 된다고 한다) \(Loss = Original\_Loss + \lambda R(W)\) 처럼 쓰고, R(W)자리에 Regularization 함수를 넣어준다. 여기서 람다는 Hyper Parameter이고, Regularization Strength를 가리킨다. 얼마나 강하게 Regularization을 적용할 것인지를 말한다.

보통 L2, L1, Max Norm Regularization, Dropout 등을 사용한다고 한다. L2는 Weight Decay라고도 불리는데 \(R(W) = \sum_k\sum_l W^2_{k,l}\)이다. 그에 비해 L1은 \(R(W) = \sum_k\sum_l \|W{k,l}\|\)이다. L1은 Sparse한 값들을 많이 만들어낸다. 문제에 따라서 적절한 것을 선택하면 된다.

Softmax

매우 흔하게 쓰인다.

확률 분포를 계산하는데, \(P(Y = k\|X=x_i) = \frac{e^{s_k}}{\sum_j e^{s_j}}\) 와 같다. 그냥 원하는 값만 exp 구한 값을 다 exp 씌우고 다 더한 값으로 나눈다.

Loss는 \(L_i = -log P(Y = y_i\|X=x_i)\)이다. Loss라서 음의 부호를 가지고, maximize가 쉬운 log를 선택했다고 설명한다. Loss가 0이 되기 위해서는 \(-logP = 0\)이어야 하는데 이는 단지 이론적으로 가능한 값이라고 한다. exp(score)가 0이 되어야 P가 0이 되는데, exp(score)가 0이라면 score가 음의 무한대이므로, 불가능하다.

Softmax vs SVM

SVM은 safety margin만 넘으면 신경쓰지 않는다는 점, Softmax는 항상 확률을 극대화시키려 한다는 점을 기억하라고 한다.

Optimization

Optimization이 매우 하기 힘든 방법이라 iterative한 방법을 많이 쓴다고 한다.

local geometry방법을 사용하는데, 매우 흔하다고 한다. Gradient를 활용한 방법이다. 강의에서는 산과 계곡, 골짜기 등으로 비유했다. 전체적인 산의 모양새를 알 수는 없지만, 땅바닥이 어느쪽으로 기울어 있는지를 판단해서 극소점을 찾아가는 방식을 생각하면 된다.

처음에 \(\frac{W + h}h\)로 작은 h값을 설정해서 일일히 W의 Gradient 전체를 구하는 방법을 알려주었는데, 이는 Debug 용으로 매우 유용하다고 한다. 그냥 미분해서 구하자.

근데, 여기서 gradient 방향으로 얼마나 갈지가 중요하다. 이를 step size라고 부르고, 또는 learning rate라고도 부른다. 물론 Hyper Parameter이다.

step size를 정하는 일이 매우 중요한데, 그 이유는 값이 너무 작으면 local minia에 갇히고, 값이 너무 크면 올바르게 minima를 찾아가지 못할 수 있기 때문이다. 그래서 많이들 처음에는 큰 값, 그리고 서서히 작아지는 값을 선택한다고 한다.

Stochastic Gradient Descent

데이터셋 전부를 순회하는 것은 느린 작업이다. 그래서 loss를 minibatch를 통해 유추한다. 보통 크기는 2^n으로 자르는데, 32, 64, 128 등등이다. Deep Neural Network에서 많이 쓴다고 한다.

Aside: Image Features

선형 분류가 불가능한 경우를 선형 분류가 가능하도록 매핑시키는 작업이라 생각하면 쉽다.

예를 들어 Color Histogram을 구한다거나, Histogram of Oriented Gradients를 구하는 것을 생각해본다. Image에서 Feature를 구한 후 그 값들로 prediction을 하고, training을 한다. 예전의 방식이고 요즘은 그냥 raw 픽셀 값으로 바로 training이 가능하다.