CS231n Lecture 2. Image Classification Pipeline
개인 공부용이고, 강의 보면서 흥미롭다 싶은 것, 다시 볼만한 것을 정리했다.
수업 전에
Assignment 1
- K-Nearest Neighbor
- Linear classifiers: SVM, Softmax
- Two-layer neural network
- Image features
일단 이거 다 듣고 만들어 봐야겠다..
Python + Numpy
python & numpy를 쓴다고 한다. python은 3.x 버전. python-numpy tutorial이 github pages에 올려져 있다고 한다. http://cs231n.github.io/python-numpy-tutorial 이것도 해보고 정리해봐야겠다.
Google Cloud
GCE를 사용하는데, GCE도 tutorial을 github pages에 올려놨다고 한다. http://cs231n.github.io/gce-tutorial 이것도 추후에 정리해봐야겠다. (이게 영상을 보면 수업할 때 구글 클라우드 지원을 받아서 숙제용으로 구글 클라우드를 사용한 것 같다.)
Image Classification

Image Classification은 위의 사진과 같이 사진을 입력으로 받아서 미리 정의된 label들 중 하나를 뽑아내는 과정이다. 사람에게는 매우 쉬워보이지만, 기계에게는 매우 어렵다. 기계는 그저 픽셀 값만을 보고 있기 때문이다. 하지만 단순히 특정 픽셀에 대응하기는 어렵다. 그 이유는 이 고양이와 카메라가 전혀 움직이지 않는다면 모르겠지만, 카메라 각도가 변할 때마다, 고양이가 움직일 때마다 대부분의 픽셀의 값이 변할 것이기 때문이다. 하지만 여전히 같은 고양이이다. 또한 빛도 고려해야 할 텐데, 고양이가 어두운 곳에 있던, 밝은 곳에 있던, 여전히 고양이이기 때문이다. 그리고 고양이가 어디 숨어있다고 해서 고양이가 아니진 않으니, 풀밭 위에서 반쯤 보이는 고양이도 고양이로 분류해야 할 것이다. (강의 영상에서는 Occlusion이라고 한다.) 뭐 그 외에도 여러가지 요인들 때문에 픽셀에 단순하게 대응하는 것은 Image Classification에 적용하기 어렵다.
그래서 나온 방법이 이미지의 edge를 뽑아내는 방법이다. 그래서 어떤 edge는 코이고, 눈이고, 입이고 등을 규칙으로 정해서 분류하는 방법인데, 이 방법도 사실 좋은 방법이라 할 수 없다. 일단 확실하다고 말할 수 없고(super brittle), 그리고 오브젝트마다 전부 규칙을 만들어내야 하기 때문이다.
그래서 Data-Driven Approach라는 접근법을 사용하는데, 다음과 같다.
- Collect a dataset of images and labels
- Use machine learning to train a classifier
- Evaluate the classifier on new images
예제로 CIFAR10이라는 dataset이 있는데, 이걸로 위에 있는 Assignment를 해보면 된다고 한다.
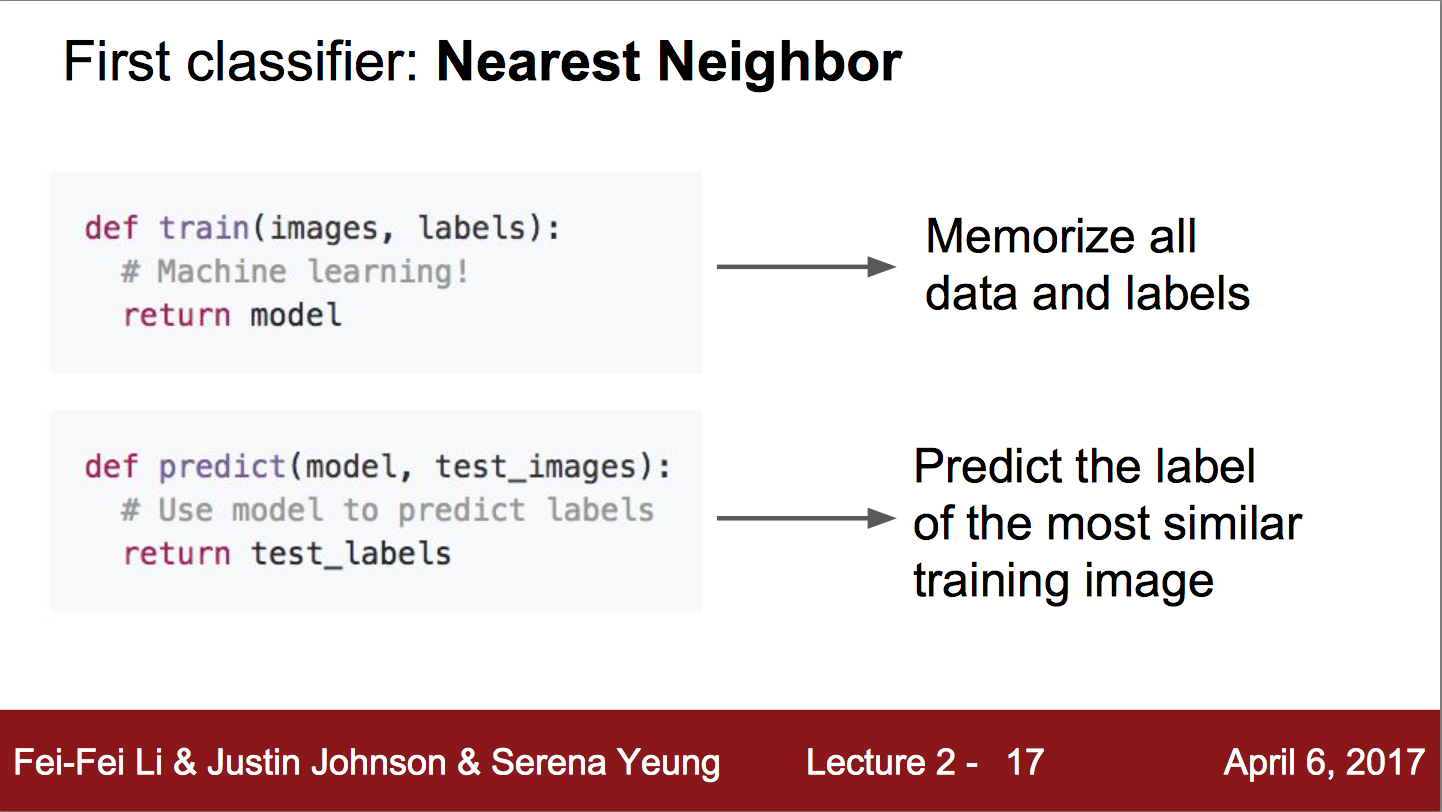
Nearest Neighbor Classifier
첫번째로 어떻게 비교할지를 결정하는 방법이다. L1 distance이다. 정말로 간단한 방법 중 하나며, 각각의 픽셀의 차를 비교하는 방법이다.
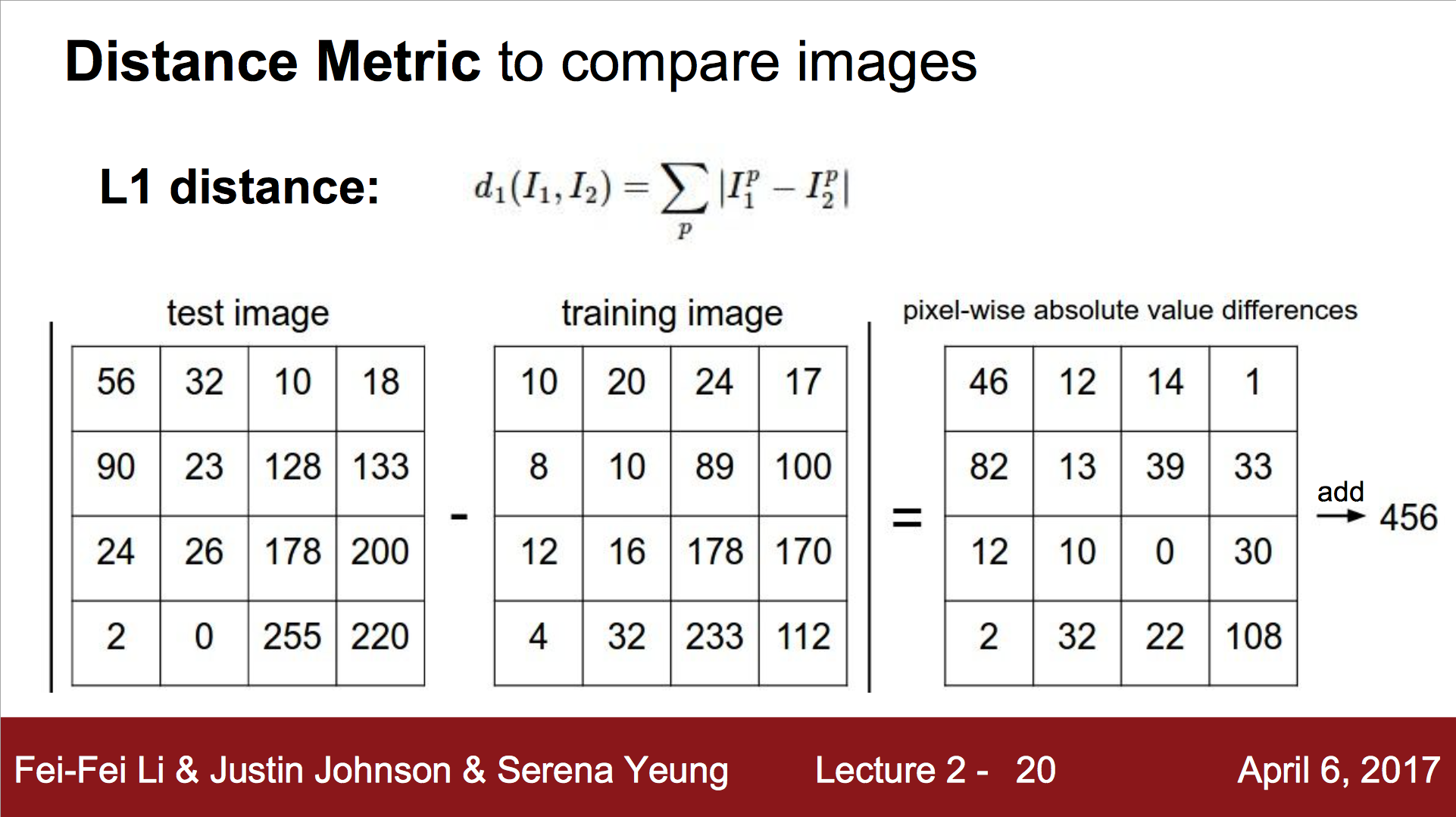
이것을 비교하는 파이썬 코드는 강의 슬라이드에 존재한다.
이 방법은 Train은 매우 빠르지만, Predict 과정은 매우 느리다. 이것은 매우 안좋은데, 그 이유는 Training이 다소 느리더라도 predict 과정에서 빠른 Classifier를 원하기 때문이다. (누가?라고 생각할 수 있지만, 당연한 말이다. 단순하게 생각해 볼 때 training한 후 predict를 반복할 때 predict가 느리면 느릴수록 predict 속도가 빠른 classifier에 비해 손해이기 때문이다. 또한 다르게 말해보자면, training을 진행한 후 배포할 때 저전력 기기라던가 뭐 다른 좋지 않은 성능의 기기에 배포한다고 생각해보면 편하다.)
성능 또한 그렇게 좋진 않은데 그 이유는 단순히 픽셀값을 비교하기 때문에 같은 label을 가지는 이미지라 하더라도 이 classifier에는 다른 카테고리로 분류될 수 있기 때문이다.
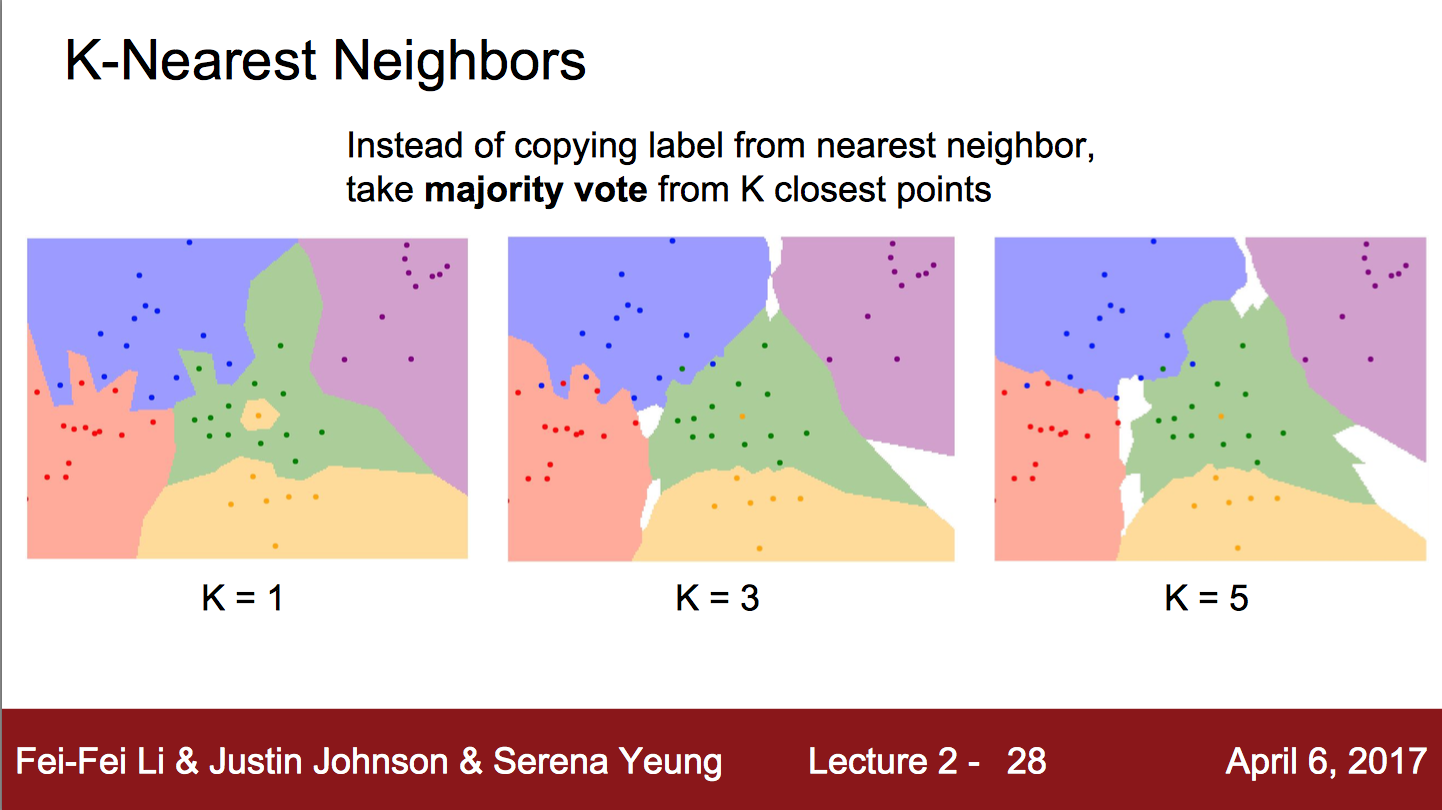
이런 방법을 쓸 때에 조정할 필요가 생기는데, 그래서 사용하는 방법이 KNN Algorithm이라고 한다.
이 방법을 사용할 땐 distance metric을 정하는데, L1과 L2가 있다. L1은 Manhattan 방법으로 다음과 같다.
\[d_1(I_1, I_2) = \sum|I^p_1 - I^p_2|\]L2 방법은 Euclidean 방법으로, 다음과 같다.
\[d_2(I_1, I_2) = \sqrt{\sum(I^p_1 - I^p_2)^2}\]이러한 KNN을 시각적으로 표현해놓은 곳이 강의자료에 링크로 나왔다. 이 곳으로 KNN Demo를 해볼 수 있다.
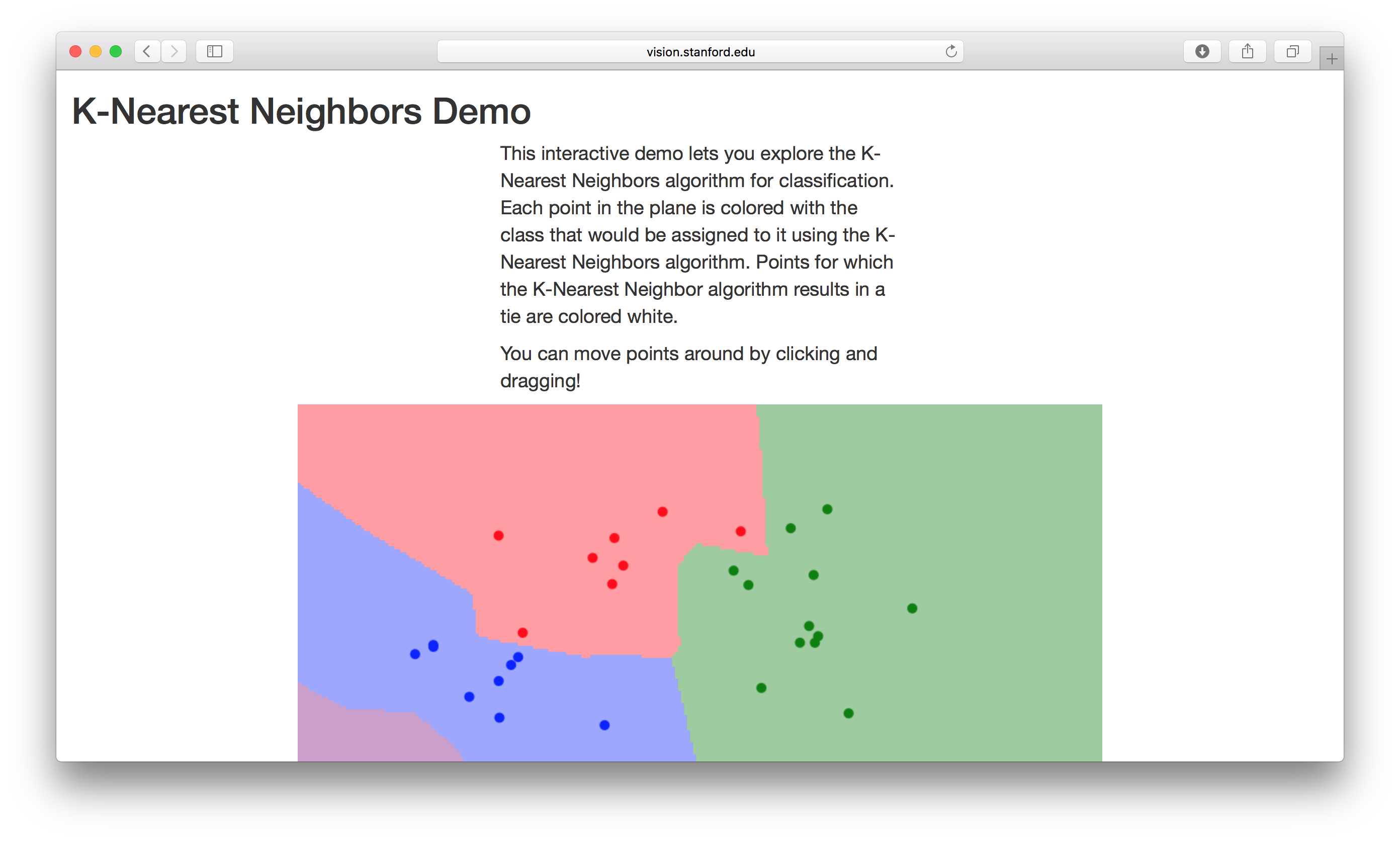
확실히 수식을 보면 알 수 있듯이 Manhattan방법은 축방향으로 많이 나누어지고, Euclidean 방법은 그렇지 않은 것 같다.
이 방법에서 distance를 정하는 방법이나, k값은 hyperparameter라고 불리는데, 이는 학습보다 알고리즘을 선택하는 parameter이기 때문이다. 그 값들은 문제들에 따라 매우 달라지며, 어떤 것을 선택할지는 그냥 해보고 제일 잘 적용되는 것을 선택하면 된다고 한다.
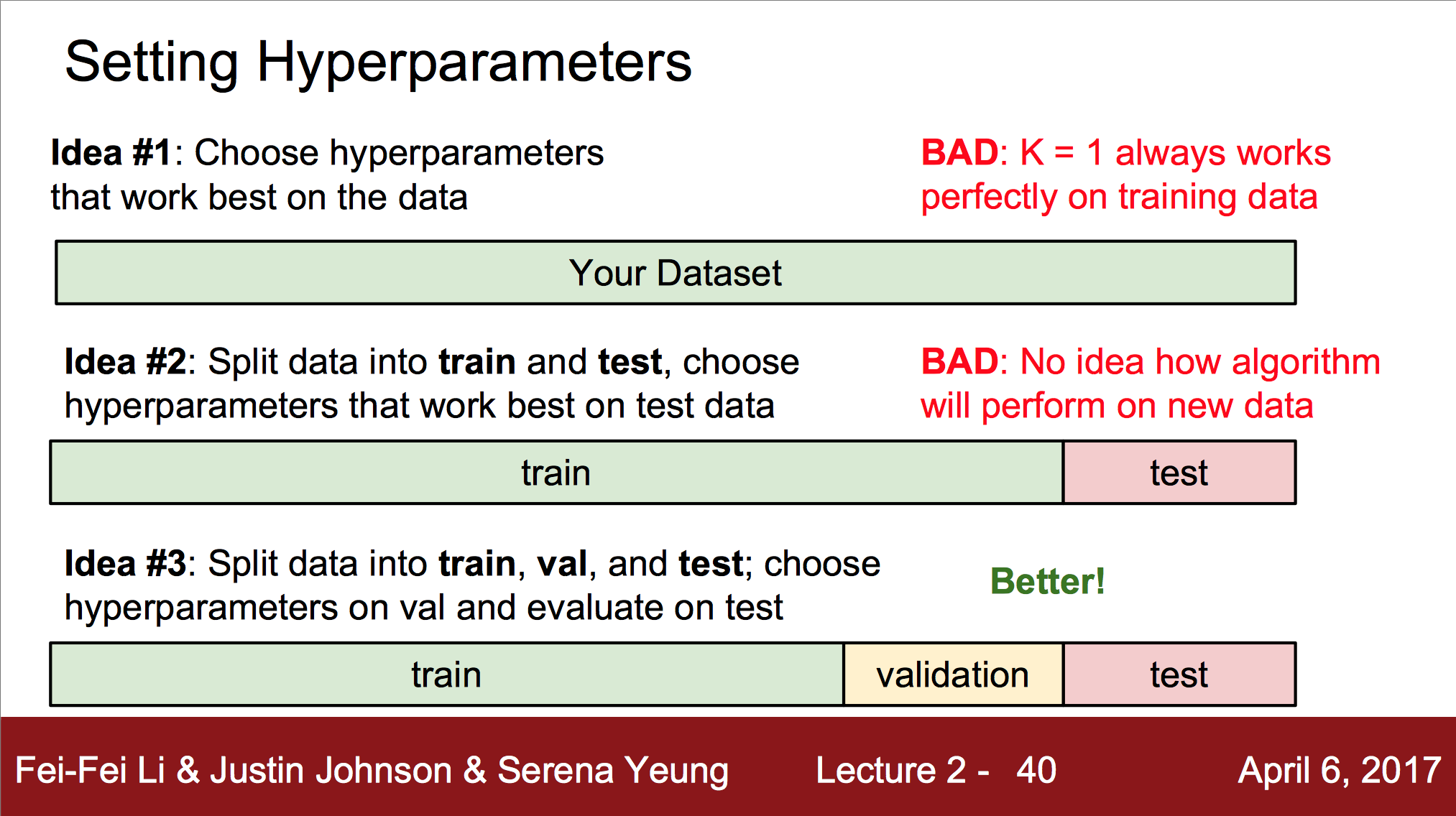
좋은 방법은 Dataset을 세개로 나눠서 학습시킨 후 validation에서 hyperparameter를 정하고 test에서 평가하는 것이라고 한다.
그 외에도 강의 슬라이드에 있는 Cross Validation도 좋은 방법이라고 한다. 하지만, deep learning에선 그렇게 많이 쓰이진 않는다고.
이렇게 많이 설명을 했지만, K-Nearest Neighbor는 이미지에 전혀 쓰이지 않는다고 한다. test time에 느리고, 픽셀의 Distance Metrics은 전혀 이득이 될 만한 정보가 없다고 한다.
Linear Classification
간단한 Learning Algorithm이지만, 이 것으로 NN, CNN 등을 이해하게 될 것이다.
이 방법을 간단하게 설명해보자면 함수로 설명할 수 있다. \( f(x, W) \) 인데 x는 이미지이고, W는 weight이다.이 함수의 결과는 10개의 카테고리로 분류하려 한다면 10개의 각각의 분류에 대한 숫자들이다. 딥 러닝은 이러한 함수 잘 쌓고 구성하여 이용하는 것이다. 다시 함수 \(f\)로 돌아가서 얘기해보자. 함수 f는 사실 다음과 같다. $ f(x, W) = Wx $ W와 x는 행렬이고, x는 32 X 32 X 3 이미지라고 하자 그 수들을 전부 이으면 3072 X 1로 재구성이 가능한데, 이 때 W를 10 x 3072의 형태로 구성한다면 결과값은 10 x 1이 된다. 그렇게 10개의 숫자를 만들어내는 것이다.
추가로 bias도 사용하는데 이것은 $ f(x, W) = Wx + b $ 의 형태로 들어가게 된다. b는 물론 \(Wx\)의 결과물과 같은 형태이다.

이러한 Linear Classification의 결과를 해석해본다면 다음과 같다.
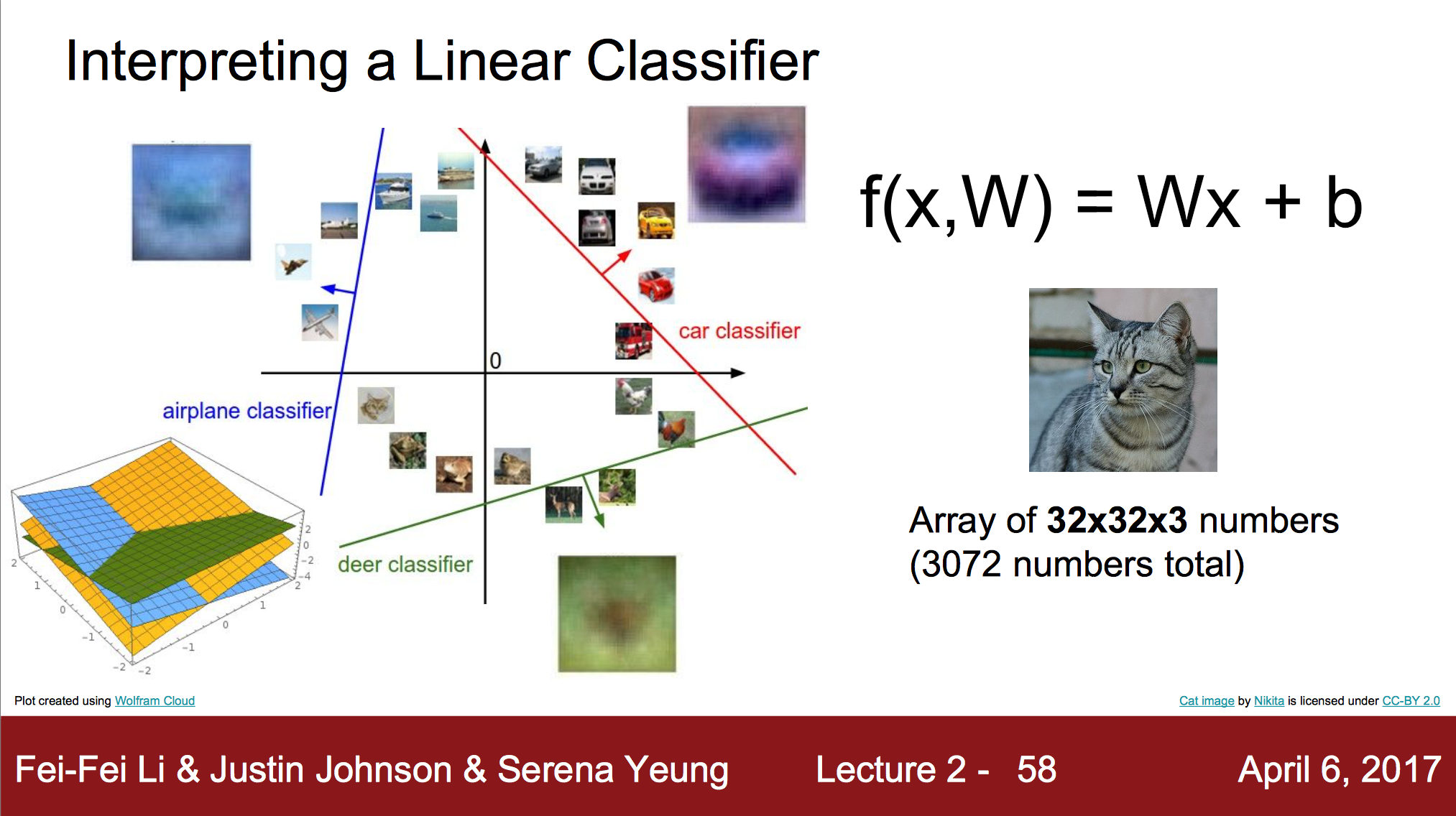
Learning을 통해 Weight와 bias값을 조절해가며 high dimensional place에 선, 면등을 그려가며 하나의 분류와 그 나머지를 분류해나간다.
그래서 이런 Linear Classification가 분류하기 어려운 경우가 존재한다.

하나의 선으로 분류하기 어려운 이런 경우가 Linear Classficiation에겐 어려운 경우이다.
다음 Lecture3에서는 Loss function, Optimization, ConvNets를 공부한다고 한다.